КАЧКИ. УРАВНЕНИЯ КАЧКИ КОРАБЛЯ КОНЕЧНЫХ РАЗМЕРОВ
Чтобы учесть конечность ширины и осадки корабля по сравнению с длиной волны (истинный профиль волны в пределах ширины и изменение давления по глубине в пределах осадки) в выражениях для возмущающих сил и моментов вводятся специальные поправочные коэффициенты. Смысл их наглядно виден из рис. 3.8 и рис. 3.9. Если мы учитываем конечность ширины, то в пределах ширины будет виден волновой профиль. При этом, например, главная составляющая возмущающей силы будет меньше, чем для бесконечно малого корабля, так как дополнительный объем, по которому определяется сила поддержания, будет меньше (заштрихованная часть). Аналогичным образом будут меньше и дифракционные члены.
Эти поправочные коэффициенты обозначим  и
и 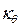 и подставим их в виде множителей перед
и подставим их в виде множителей перед 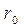 и
и  соответственно. Величины этих коэффициентов находятся в пределах от 0 до 1. Для корабля бесконечно малых размеров
соответственно. Величины этих коэффициентов находятся в пределах от 0 до 1. Для корабля бесконечно малых размеров  =1 и
=1 и  =1 .
=1 .
В теории качки существует большой раздел, посвященный определению этих коэффициентов. По предложению Г.Е. Павленко специалисты пред-ставляют в виде  и
и  , т. е. разделяют влияние конечности ширины (коэффициенты
, т. е. разделяют влияние конечности ширины (коэффициенты 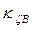 и
и 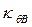 ) и конечности осадки (коэф-фициенты
) и конечности осадки (коэф-фициенты 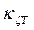 и
и 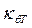 ).
).
Для корабля, у которого обводы корпуса близки к параболическим, при расчете поправочных коэффициентов можно использовать следующие формулы:

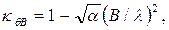 (3.37) где
(3.37) где 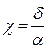 - коэффициент вертикальной полноты,
- коэффициент вертикальной полноты,  - коэффициент общей полноты,
- коэффициент общей полноты, 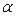 - коэффициент полноты площади ВЛ.
- коэффициент полноты площади ВЛ.
В 6 разделе приведен способ определения 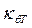 с помощью вспомогательных графиков, просчитанных заранее.
с помощью вспомогательных графиков, просчитанных заранее.
Для удобства дальнейших рассуждений обычно заменяются
 и
и 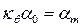 , (3.38)
, (3.38)
где 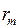 - приведенный радиус орбитального движения частиц воды,
- приведенный радиус орбитального движения частиц воды,  - приве-денный максимальный угол волнового склона.
- приве-денный максимальный угол волнового склона.
Таким образом, уравнения качки корабля конечных размеров на волнении будут иметь вид:
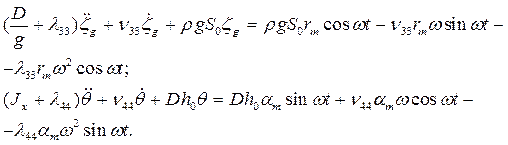 (3.39)
(3.39)
Эти уравнения имеют универсальный характер, так как для бесконечно малого корабля 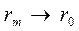 ,
, 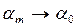 , и уравнения автоматически пре-вращаются в уравнения (3.33) и (3.36).
, и уравнения автоматически пре-вращаются в уравнения (3.33) и (3.36).
Дата добавления: 2015-03-11; просмотров: 821;
