Практическое правило

Чтобы определить компасный курс по истинному, из последнего надо алгебраически вычесть вариацию (склонение и девиацию).

Пример:

D = 11° NW; d = 5° NW; ИК = 216°.

Подсчитаем Va, МК и КК.

Va = (–11°) + (–5°) = –16° (NW); МК = ИК – D = 216° – (–11°) = 227°;

KK = MK – Va = 216° – (–16°) = 232°.

Чтобы определить истинный курс по компасному, к последнему надо алгебраически прибавить вариацию.

Пример:

D = 12° NW; d = 3° NO; KK = 118°.

Подсчитаем Va, МК и ИК.

Va = (–12°) – (–3°) = –9 (NW); MK = KK + d = 118° + 3 = 121°;

ИК = 118° + (–9°) = 109°.

Производя компенсацию компаса при помощи дополнительных магнитов, можно уменьшить девиацию до 3–4° и даже меньше.

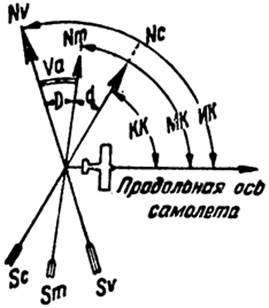
Рис. 36. Курс.

Если используемый компас компенсирован полностью, то учитывать надо только склонение. При этом правила расчета, данные выше, упрощаются следующим образом:

1) при переходе от истинного курса к компасному склонение алгебраически вычитают;

2) при переходе от компасного курса к истинному склонение алгебраически прибавляют.

Например, мы располагаем компасом, имеющим шкалу в 360°; склонение в нашем районе западное — 11°. В этом случае для полета на истинный север необходимо метку компаса совместить с 11° на картушке; при полете на юг метку компаса надо совместить с 191° на картушке.

Обратно: если летчик видит, что метка компаса совмещена с 11° картушки, то самолет летит на север, если же эта метка совмещена с 191°, то самолет летит на юг.

В некоторых вертикальных компасах картушка имеет цилиндрическую форму, и отсчет делается по отметке сбоку или позади котелка. Шкала этих картушек обратна обычным.

Если начальная часть маршрута нам известна или если сразу же после вылета мы находим нужный нам ориентир, то можно (по крайней мере в первой части пути) избежать всех указанных выше вычислений: мы направляем самолет по найденному ориентиру, читаем курс компаса и сохраняем его.

КАРТА

Мы видели, что компас позволяет так управлять самолетом, чтобы путь его составлял некоторый угол с направлением на север. Для этого достаточно совместить продольную ось самолета с соответствующим делением на компасной картушке.

Предположим, что надо перелететь из точки А в точку В. Соединим на карте эти точки прямой, которая соответствует пути следования. Определим углы, которые образует на карте эта прямая с географическим севером, или, как говорят, с меридианами.

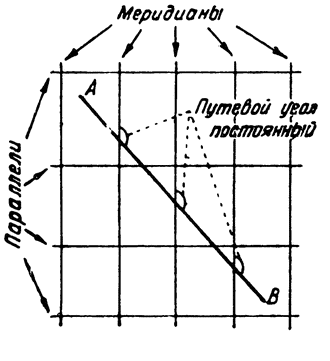
1. На карте, вычерченной в проекции Меркатора (рис. 37), наша прямая пересекает все меридианы под одним и тем же углом, так как линии меридианов параллельны между собой.

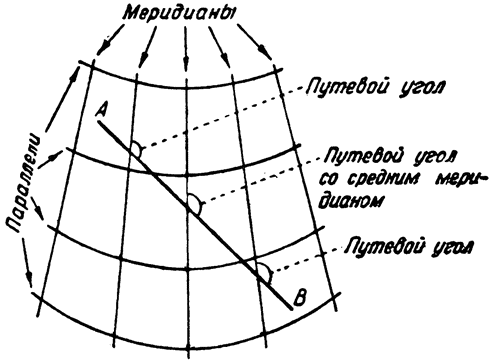
2. На карте, вычерченной в иной проекции (рис. 38), этого уже не будет, так как линии меридианов не параллельны. Однако для маршрутов менее 500 км, этот угол изменяется очень мало, и в качестве путевого угла можно брать угол, который образует прямая АВ с средним меридианом (с тем, который расположен на одинаковом расстоянии от А и В).

Рис. 37. Проекция Меркатора.	Рис. 38. Поликоническая проекция.

Масштаб дает отношение между расстояниями на карте и соответствующим расстоянием на земле. Таким образом, масштаб ¹/₂₀₀₀₀₀ обозначает, что 1 мм на карте соответствуют 200 000 мм (200 м) на земле, масштаб в ¹/₅₀₀₀₀₀ обозначает, что 1 мм на карте соответствуют 500 000 мм (500 м) на земле.

Карта генерального штаба в ¹/₂₀₀₀₀₀ слишком громоздка, но очень удобна для выбора посадочных площадок; эта карта вычерчена в проекции Меркатора. Расстояния на ней указаны в километрах и масштаб вынесен на поля.

Карта в ¹/₅₀₀₀₀₀ (построенная в проекции, отличной от проекции Меркатора) наиболее удобна.

Картой в ¹/_1000000 (также не в проекции Меркатора) могут пользоваться только опытные летчики¹.