СКОРОСТЬ. ВЕТЕР. СНОС
Скорость равна пути, проходимому в единицу времени. Если взять в качестве единицы час, то скорость будет равна пути, пройденному в 1 час. Графически скорость представляют в виде отрезка прямой, пропорционального скорости и направленного в сторону движения (вектора) (рис. 41 и 42).
Различают:
1. Воздушную скорость самолета (Vp), которая является скоростью относительно воздушной среды. Эта скорость определяется указателем скорости.
2. Путевую скорость самолета (Vv), которая является скоростью относительно земли.
Ветер, в зависимости от его направления, влияет или на путевую скорость самолета, или на путь, или на то и другое. Если ветер попутный, то скорость ветра складывается с собственной скоростью самолета; при встречном ветре скорость ветра вычитается; при боковом ветре изменяются и скорость, и направление следования самолета.
Если летчик хочет прибыть в пункт назначения по прямой, он должен лететь под некоторым углом по отношению к ветру; этот угол называется углом сноса.
Самолет, летящий при ветре данной силы, отклоняется тем больше, чем ближе направление ветра к перпендикулярному. Этот эффект тем больше, чем больше скорость ветра и чем меньше скорость самолета. При ветре, дующем перпендикулярно к пути со скоростью 10 м/сек, самолет, летящий со скоростью (путевой) 150 км/час, отклоняется в сторону на 13°.
Отсюда видна необходимость для летчика уметь подсчитать поправку, позволяющую устранить влияние ветра. Для этого ему необходимо знать, хотя бы приближенно, направление и скорость ветра.
В воздухе отклонение самолета определяется летчиком путем сличения карты с местностью; однако летчик, учитывая возможность вынужденной посадки, всегда должен наблюдать за признаками, которые могут указать ему направление ветра относительно земли (дым над селениями, пыль на дорогах и т. д.). Над морем летчик должен наблюдать пену на гребнях волн, движение встречающихся парусных судов или дым от сбрасываемых с самолета дымовых патронов.
Вот две основные задачи, возникающие при полете с ветром.
1-я задача.
Пусть даны: истинный курс и воздушная скорость самолета, направление и скорость ветра. Определить фактический путевой угол и путевую скорость самолета.
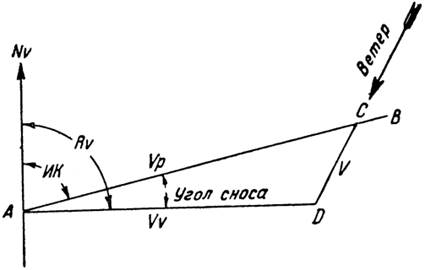
Предположим (рис. 41), что самолет идет определенным истинным курсом из точки А к точке В, расположенной на востоке; его воздушная скорость равна 180 км/час. После часового полета он был бы в точке С, если бы воздух был неподвижен (расстояние АС равно 180 км): фактический путевой угол (сокращенно Rv) должен был бы совпадать с ИК (истинный курс).
|
| Рис. 41. |
Если дует северо-восточный ветер со скоростью 10 м/сек (или 36 км/час), то самолет переместится, во-первых, на 180 км к востоку и, во-вторых, на 36 км к юго-западу. После часового полета он прибудет таким образом в точку D, следуя по истинному пути AD.
Угол DAC есть угол сноса; сторона AD, взятая в том же масштабе, что и две остальные стороны треугольника, представляет путевую скорость самолета.
2-я задача.
Какой истинный курс надо задать самолету, чтобы лететь по заданному пути АВ, если известны воздушная скорость самолета и ветер?
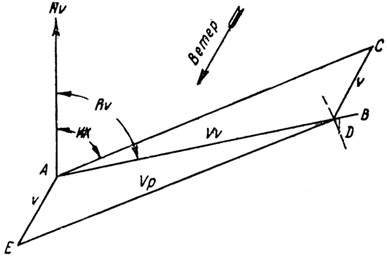
Проведем из точки А (рис. 42) вектор АЕ, представляющий ветер v. Из точки Е, как из центра, опишем дугу радиусом Vp. Эта дуга пересекает АВ в точке D. Из точки А проведем прямую, параллельную ED, а из точки D — прямую, параллельную ЕА. Мы получили, таким образом, еще точку С. АС равно ED, и, следовательно, равно Vp. CD равно АЕ и, следовательно, равно v. ACD является треугольником скоростей, третья сторона которого AD представляет путевую скорость. Для следования по пути АВ надо направить самолет истинным курсом (ИК), определяемым углом между Nv и прямой АС.
Это построение легко производить на бумаге, разграфленной на квадраты, с учетом величины векторов Vp и v (принимая, например, масштаб 10 км в одном делении).
|
| Рис. 42. |
Линию АВ обычно наносят посредством транспортира. Когда график закончен, с помощью транспортира определяют нужный истинный курс (ИК).
Скорость ветра, выраженную в метрах в секунду, можно преобразовать в скорость, выраженную в километрах в час; для этого ее надо умножить на коэфициент 3,6 (пример: 8 м/сек равно 28,8 км/час).
Время, выраженное в часах, минутах и секундах, выражено не в десятичной системе. Перед всеми действиями надо преобразовать время в десятичную систему. Так, например, 10 ч. 15 м. выражаются в десятичной системе как 10,25. Для перехода надо число минут разделить на 60, тогда получается десятичная дробь:
| ( | = 0,25 | ). |
Если в подсчете встречаются минуты и секунды, надо преобразовать секунды в десятичную дробь минут, минуты с дробями преобразовать в дробные части часов тем же действием:
Пример:
1 час 15 минут 36 секунд.
| 36 секунд = | = 0,6 минуты; |
| 15,6 минуты = | 15,6 | = 0,26 часа, |
откуда 1 час 15 минут 36 секунд = 1,26 часа.
Наоборот, время, выраженное в часах с дробью, преобразуется в часы, минуты и секунды противоположным действием (умножением на 60)1.
Пример:
1.25 часа = 1 час + (0,25 × 60) = 1 час 15 минут.
1.26 часа = 1 час + (0,26 × 60) = 1 час 15,6 минуты.
1 час + 15 минут + (0,6 × 60) = 1 час 15 минут 36 секунд.
Дата добавления: 2014-12-18; просмотров: 1517;
