Перевірка випадковості коливань рівнів залишкової послідовності

Означає перевірку гіпотези про правильність вибору виду тренда. Для дослідження випадковості відхилень від тренда ми маємо у своєму розпорядженні набір різниць:

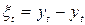(t=1,2,…,n).

Характер цих відхилень вивчається за допомогою ряду непараметричних критеріїв. Одним з таких критеріїв є критерій серій, заснований на медіані вибірки. Ряд з величин розташовують у порядку зростання їхніх значень і знаходять медіану 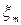отриманого варіаційного ряду, тобто серединне значення при непарному n або середню арифметичну із двох серединних значень при n парному. Вертаючись до вихідної послідовності 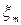й порівнюючи значення цієї послідовності з 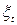, будемо ставити знак "плюс", якщо значення 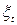перевершує медіану, і знак "мінус", якщо воно менше медіани; у випадку рівності порівнюваних величин відповідне значення 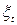опускається. Таким чином, виходить послідовність, що складається із плюсів і мінусів, загальне число яких не перевершує n. Послідовність підряд, що йдуть плюсів, або мінусів називається серією. Для того щоб послідовність 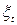була випадковою вибіркою, довжина самої довгої серії не повинна бути занадто великий, а загальне число серій − занадто малим.

Позначимо довжину самої довгої серії через К_мах, а загальне число серій − через v. Вибірка зізнається випадкової, якщо виконуються наступні нерівності для 5%-ного рівня значимості:

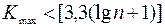
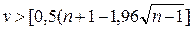
де квадратні дужки, як звичайно, означають цілу частину числа.

Якщо хоча б одна з нерівностей не виконується, то гіпотеза о випадковім характері відхилень відкидається і модель вважається не адекватною.

Іншим критерієм для даної перевірки може служити критерій піків (поворотних крапок). Рівень послідовності е( уважається максимумом, якщо він більше двох рядом вартих рівнів, Т.ч. 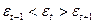, і мінімумом, якщо він менше обох сусідніх рівнів, тобто 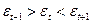. В обох випадках уважається поворотною точкою; загальне число поворотних точок для залишкової послідовності позначимо через р.

У випадковій вибірці математичне очікування числа крапок повороту 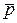і дисперсія σ²_р виражаються формулами:

;

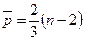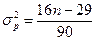
Критерієм випадковості з 5%-ним рівнем значимості, тобто з довірчою ймовірністю 95%, є виконання нерівності

,

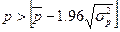де квадратні дужки, як і раніше, означають цілу частину числа.

Якщо нерівність не виконується, модель вважається не адекватною.