Преобразования Лоренца.

Из постулатов СТО вытекают новые формулы для преобразования координат и времени. Эти формулы получили название преобразований Лоренца. Запишем преобразования Лоренца для частного случая двух инерциальных систем отсчета, движущихся относительно друг друга со скоростью 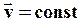вдоль оси x.

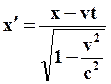
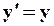
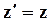
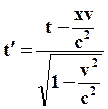
(65)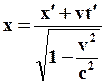

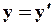
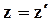
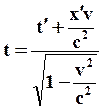
(66)

Рассмотрим следующие случаи:

1) Пусть скорость v гораздо меньше скорости света c в вакууме. Если v<<c, то 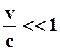, 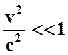и из (65) получим преобразование Галилея (61)

; ; ;

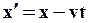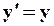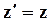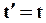
Следовательно, преобразования Галилея верны только для случая малых скоростей и являются частным случаем преобразований Лоренца.

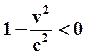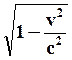2) Пусть v>c. В классической механике считалось, что тела могут двигаться с любыми сколь угодно большими скоростями. Из преобразований Лоренца следует, что при v>c и становится мнимым, а координаты и время теряют физический смысл.

Таким образом, скорость света в вакууме является предельной скоростью распространения взаимодействий в природе.