Принцип относительности в механике.
Ранее было введено понятие инерциальных систем отсчета, в которых выполняются законы Ньютона. Оказалось, что инерциальных систем отсчета существует бесчисленное множество.
Покажем, что любая система, движущаяся относительно инерциальной с постоянной по величине и направлению скоростью, тоже является инерциальной. Для этого рассмотрим 2 системы отсчета:
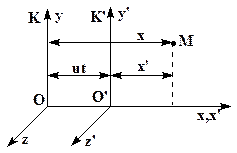
| К – неподвижная инерциальная система отсчета;
K’ – система, движущаяся относительно инерциальной с постоянной скоростью 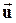 по оси x.
Выберем некоторую точку M и обозначим:
x,y,z – координаты точки M в системе K,
|
x’,y’,z’ – координаты т. M в системе K’.
Выразим координаты этой точки в движущейся системе отсчета через координаты ее в неподвижной системе, предполагая, что в начальный момент времени точки O и O’ совпадали. Из рисунка видно, что:
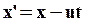
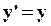
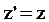
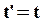
| (61) |
Эти соотношения называют соотношениями Галилея. Продифференцируем (61) по времени:
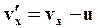
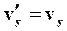
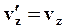
| (62) |
Запишем (62) в векторной форме:
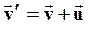(63)
Соотношения (62) и (63) называются классическим законом сложения скоростей.
Продифференцируем по времени (63):
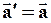(64)
Таким образом, ускорение тела по отношению к различным инерциальным системам отсчета одинаково.
Поэтому, если система Kинерциальна (в отсутствии внешних воздействий на т. M ее ускорение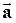 
равно нулю), то и система K’ тоже является инерциальной ( 
).
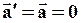Из (64) следует, что силы, действующие на тело, одинаковы во всех инерциальных системах отсчета. В самом деле,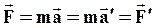 
. Это значит, что во всех инерциальных системах отсчета механические явления протекают одинаково, а законы Ньютона не меняются при переходе от одной инерциальной системы к другой. Говорят, что законы Ньютона инвариантны относительно преобразований Галилея.
Принцип относительности Галилея:
никакими механическими опытами, проведенными в замкнутой системе отсчета, нельзя установить, движется эта система прямолинейно и равномерно или покоится.
Дата добавления: 2014-12-09; просмотров: 715;