Энергия упругой волны. Плотность энергии.

Пусть в среде вдоль оси x распространяется плоская волна:

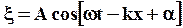
Выделим малый объем DV среды, масса которого M=rDV, где r - плотность среды.

Все точки этой среды совершают колебания со скоростью u:

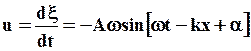
Кинетическая энергия частицы 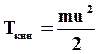, кинетическая энергия всех частиц среды в объеме DV

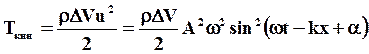(65)

Кинетическая энергия выделенного объема меняется с течением времени, поэтому найдем среднее значение ее за период 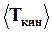. Т.к. среднее за период значение квадрата синуса равно 1/2, то

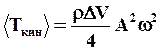(66)

Частицы среды, совершающие колебательное движение, обладают не только кинетической, но и потенциальной энергией U. Ранее было показано, что средние за период значения кинетической и потенциальной энергии ГО одинаковы. Аналогично, в случае среды, в которой распространяется волна:

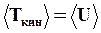(67)

Тогда среднее значение за период энергии среды в объеме DV при распространении в ней волны будет равно:

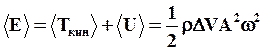(68)

Энергия упругой волны, заключенная в единице объема называется объемной плотностью энергии волны.

Разделив (24) на DV, получим среднюю за период объемную плотность энергии волны:

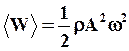(69)