Определение степени свободы и геометрической неизменяемости плоских систем

В строительной механике при решений задач расчета реальных сооружений на прочность, жесткость и устойчивость вместо самого сооружения рассматривается его упрощенное изображение, свободное от второстепенных, не играющих существенной роли в работе сооружения факторов, называемое расчетной схемой. В дальнейшем для краткости расчетную схему будем называть сооружением и ограничимся рассмотрением лишь сооружений в виде плоских систем, составленных из отдельных элементов, связанных между собой. Такие системы могут воспринимать нагрузку лишь в том случае, если они сохраняют заданную им при возведении внутреннюю структуру, т. е. геометрическую форму и положение. Изменяемые системы не в состоянии уравновесить внешние силы и под их действием приходят в движение, меняют свою форму. Естественно, что такие системы нельзя использовать в качестве сооружений. Другими словами, сооружение должно быть структурно, или геометрически неизменяемым (т.е.изменение его формы возможно лишь за счет деформации элементов) и неподвижным относительно основания. Для выяснения того, обладает ли данная система этой способностью, какими условиями она обеспечена, а также для уяснения роли, которую играют отдельные элементы в работе сооружения, служит кинематический анализ, который должен предшествовать расчету.

Изменяемость внутренней структуры и подвижность сооружения относительно основания характеризуются его степенью свободы – числом независимых геометрических параметров, определяющих положение всех элементов сооружения. Поэтому кинематический анализ сооружения начинается с определения его степени свободы.

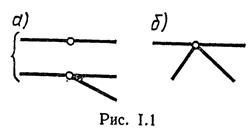Каждый структурно (геометрически) неизменяемый элемент соору­жения, называемый диском, имеет на плоскости три степени свободы, так как он может перемещаться поступательно в двух направлениях и поворачиваться вокруг любой точки. Простейшим диском является стержень. Для обеспечения неизменяемости структуры и неподвижности сооружения диски соединяют различными устройствами, ограничивающими степень свободы. Всякое устройство, отнимающее у тела одну степень свободы, называется кинематической связью. В качестве связей используют шарниры и опоры. Шарниры бывают простыми (рис.1.1,а) и кратными (рис.1.1,б). Простой шарнир соединяет два диска, кратный — более двух и эквивалентен (п — 1) простым шарнирам, где п - число соединяемых дисков. Каждый простой шарнир экви­валентен двум связям, так как препятствует любым двум взаимным ли­нейным смещениям двух дисков, оставляя возможность взаимного их поворота. Различают следующие типы расчетных схем опор (рис. 1.2): а - цилиндрическая подвижная, или шарнирно подвижная, б - цилиндрическая неподвижная, или шарнирно неподвижная,

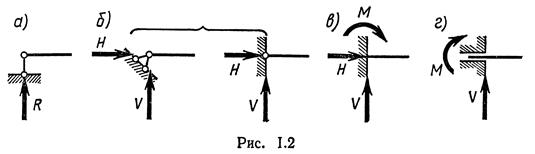
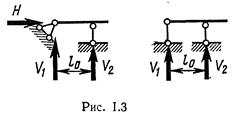в - защемляющая неподвижная, или жесткая заделка, г - защемляющая подвижная, или скользящая заделка, эквивалентные соответственно одному, двум, трем и двум опорным стержням, в каждом из которых действует опорная реакция. На рис. 1.3 показаны шарнирно-стержневые эквиваленты жесткой и скользящей заделок. Здесь расстояние l₀ назы­вается глубиной заделки, а произведение V₂l₀= М — опорным мо­ментом или моментом в заделке. Каждый опорный стержень эквитвалентен одной связи, так как препятствует перемещению диска в направлении стержня.

Из сказанного выше следует, что степень свободы W сооружения, состоящего из Д дисков, соединенных Ш простыми шарнирами и име­ющего С₀ опорных стержней, может быть определена по формуле П.Л.Чебышева:

W = 3Д — 2Ш — С₀. (1.1)

Для определения числа Д необходимо предварительно отбросить все шарниры и опоры, а для определения числа Ш — все опоры.

Для шарнирно-стержневых систем (ферм), т. е. систем, состоящих из стержней, соединенных между собой по концам шарнирами (причем каждый стержень прикрепляется к соседним только двумя шарнирами), степень свободы может быть определена по более простой формуле:

W = 2У – С – С₀, (1.2)

где У — число узлов фермы; С — число внутренних стержней фермы; С_о — число опорных стержней. Эта формула получена исходя из того, что каждый узел, как точка, имеет на плоскости две степени свободы, а каждый стержень, соединяющий два узла, или опорный эквивалентны одной связи, так как налагает на координаты этих точек единственное условие — постоянство расстояния.

Степень свободы системы, не имеющей опорных стержней, скла­дывается из двух частей: степени изменяемости внутренней структуры системы и степени подвижности ее относительно основания, которая равна трем. Обозначая степень изменяемости структуры системы через И, можно записать

И = W – 3 = 3Д – 2Ш – 3 (1.3)

или для шарнирно-стержневых систем

И = 2У – С – 3 (1.4)

Для системы, имеющей опорные стержни, не делают различия между степенью свободы и степенью изменяемости, рассматривая основание в качестве диска, связанного с сооружением опорными стержнями.

При определении степени свободы или степени изменяемости системы возможны следующие три качественно различных результата:

1. W > 0 или И > 0 — система структурно изменяемая, так как не имеет достаточного количества связей. Система, для которой W = 1 или И = 1, называется механизмом.

2. W = 0 или И = 0 — система обладает необходимым минимумом связей, чтобы быть неподвижной и неизменяемой.

3. W < 0 или И < 0 — система имеет лишние связи.

Аналитические условия W ≤ 0 или И ≤ 0 являются необходимыми, но недостаточными для суждения о неизменяемости и неподвижности сооружения, так как эти характеристики зависят не только от числа связей, наложенных на диски, но и от их расположения. Для того чтобы узнать, является ли сооружение действительно неизменяемым и неподвижным, а также выяснить, какую роль играют отдельные элементы в его работе, необходимо произвести анализ структуры сооружения, для чего нужно знать принципы образования структурно неизменяемых систем. Перечислим основные из них:

1. Присоединение к неизменяемой системе двухстержневого звена (диады) не изменяет степени свободы системы (рис. 1.4, а).

2. Два диска могут быть соединены жестко с помощью шарнира С и стержня АВ, ось которого не проходит через центр шарнира (рис. 1.4, б).

3. Два диска могут быть соединены жестко тремя стержнями, непересекающимися в одной точке и, следовательно, не параллельными (рис. 1.4, в). Этот принцип может быть сведен к предыдущему, поскольку два стержня всегда могут быть заменены фиктивным шарниром, расположенным в точке пересечения этих стержней.

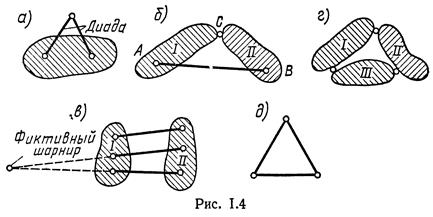
4. Три диска можно соединить жестко с помощью трех шарниров, не лежащих на одной прямой (рис. 1.4, г).

Все перечисленные принципы могут быть сведены к одному: шарнирно-стержневой треугольник (рис. 1.4, д) — фигура структурно, т. е. геометрически, неизменяемая.