Второй закон термодинамики

Второй закон термодинамики устанавливает критерии, позволяющие определить направление самопроизвольного протекания процессов.

Самопроизвольными называют процессы, которые протекают в системе без затраты энергии извне.

Процессы бывают обратимыми и необратимыми. Необратимые процессы идут самопроизвольно лишь в одном направлении. После протекания данных процессов, сопровождающихся изменениями в системе и окружающей среде, невозможно вернуть одновременно и систему и окружающую среду в исходное состояние.

Обратимыми являются процессы, после которых систему и окружающую среду можно вернуть в исходное состояние.

Второй закон термодинамики имеет несколько формулировок, в варианте, предложенном Клаузиусом, он выглядит следующим образом: невозможен самопроизвольный переход теплоты от холодного тела к горячему.

Физический смысл второго закона термодинамики заключается в том, что любой самопроизвольный процесс протекает в направлении, при котором система из менее вероятного состояния переходит в более вероятное состояние. Другими словами, самопроизвольному протеканию процесса способствует увеличение неупорядоченности в системе.

Для характеристики меры неупорядоченности используется термодинамическая функция – энтропия S, которая связана с термодинамической вероятностью системы формулой Больцмана:

S = k · lnW, (25)

где k – постоянная Больцмана.

Под термодинамической вероятностью W понимают число равновероятных микроскопических состояний, которыми может быть реализовано данное макроскопическое состояние системы. Для определения термодинамической вероятности системы необходимо найти число различных вариантов положений всех частиц системы в пространстве.

Энтропия является количественной мерой беспорядка в системе. Чем больше W, тем хаотичнее система, тем больше величина энтропии. Нагревание вещества приводит к увеличению энтропии, а охлаждение – к уменьшению. При приближении к абсолютному нулю (-273ºС) энтропия стремится к нулю, что позволяет определить абсолютные значения энтропии различных веществ, значения которых при стандартных условиях представлены в таблицах. Следует отметить, что в отличие от энтальпии образования, энтропия простого вещества, даже находящегося в кристаллическом состоянии, не равна нулю, т.к. при температуре, отличающейся от абсолютного нуля, макросостояние кристалла может быть реализовано не единственным макросостоянием, а большим числом равновероятных состояний.

Другая формулировка второго закона термодинамики выглядит так: полная энтропия всегда увеличивается в самопроизвольном процессе.

Увеличение энтропии ΔS при протекании процесса должно превышать или быть равным отношению количества теплоты Q, переданного системе, к температуре Т, при которой теплота передаётся:

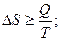
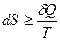. (26)

Уравнение (26) является математической записью второго начала термодинамики. В данном уравнении знак неравенства относится к необратимым самопроизвольным процессам, а знак равенства – к обратимым процессам.

Согласно уравнению (26), изменение энтропии при обратимом переходе системы из состояния 1 в состояние 2 можно определить как:

ΔS = S₂ – S₁ = 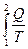. (27)

Фазовые переходысопровождаются тепловым эффектом, называемым теплотой фазового перехода ΔН_ф.п., и являются изотермическими процессами (Т_ф.п.= const). Для фазового перехода одного моля вещества изменение энтропии равно:

ΔS_ф.п.= 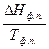. (28)

В процессах плавления, испарения жидкости или сублимации вещества энтропия увеличивается, так как разрушается упорядоченная кристаллическая решётка. Обратные процессы: кристаллизации, конденсации, десублимации сопровождаются уменьшением неупорядоченности в системе, и следовательно, уменьшением энтропии.

При изменении температурывещества от Т₁ до Т₂ при постоянном давлении изменение энтропии определяется по формуле:

ΔS = 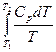, (29)

поскольку С_р = const, то

ΔS = С_р· ln 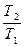. (30)

Для изохорных процессов

ΔS = 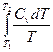, (31)

при С_v = const

ΔS = С_v· ln 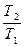. (32)

Стандартной энтропией ΔS 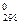называется энтропия 1 моля вещества в стандартных условиях. Изменение стандартной энтропии ΔS 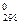при протекании химической реакции можно рассчитать по уравнению, основываясь на следствии из закона Гесса:

ΔS 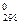= 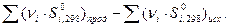(33)

Наиболее хаотичной формой вещества является газообразное состояние, поэтому если в результате химической реакции число молей газа увеличивается, то хаотичность, а следовательно, и энтропия системы возрастает.

Обычно определяют не абсолютн6ое значение энтропии, а её изменение (S₂ – S₁) в том или ином процессе. Для вычисления изменения энтропии при переходе одного моля идеального газа из одного состояния в другое используют формулы:

S₂ – S₁ = R 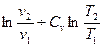(34)

S₂ – S₁ = R 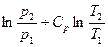(35),

где С_р и С_v – постоянные величины. Изменение энтропии при нагревании единицы массы вещества, находящегося в твёрдом или жидком состоянии, рассчитывают по формуле:

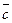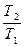S₂ – S₁ = ln (36),

где 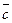- удельная теплоёмкость вещества.

При переходе вещества из одного агрегатного состояния в другое изменение энтропии определяется по формуле:

S₂ – S₁ = 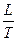(37),

где L – скрытая теплота обратимого фазового перехода (испарения, плавления и др.); Т – температура фазового перехода.