ПОСЛЕДОВАТЕЛЬНЫЕ ИСПЫТАНИЯ. ФОРМУЛА БЕРНУЛЛИ.

Предположим, что производится n независимых испытаний, в результате каждого из которых может наступить или не наступить некоторое событие A. Пусть при каждом испытании вероятность наступления события А равна P(A)=p и, следовательно, вероятность противоположного события (ненаступления А) равна 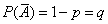. Определим вероятность Pn(m) того, что событие А произойдет m раз при n испытаниях. При этом заметим, что наступления или ненаступления события А могут чередоваться различным образом. Условимся записывать возможные результаты испытаний в виде комбинаций букв А и 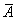. Например, запись 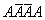означает, что в четырех испытаниях событие осуществилось в 1-м и 4-м случаях и не осуществилось во 2-м и 3-м случаях.

Всякую комбинацию, в которую А входит m раз и 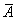входит n-m раз, назовем благоприятной. Количество благоприятных комбинаций равно количеству k способов, которыми можно выбрать m чисел из данных n; таким образом, оно равно числу сочетаний из n элементов по m, т.е.

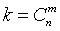
Подсчитаем вероятности благоприятных комбинаций. Рассмотрим сначала случай, когда событие A происходит в первых m испытаниях и, следовательно, не происходит в остальных n-m испытаниях. Такая благоприятная комбинация имеет следующий вид:

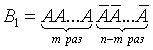
Вероятность этой комбинации в силу независимости испытаний (на основании теоремы умножения вероятностей) составляет

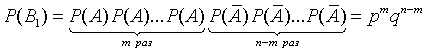
Так как в любой другой благоприятной комбинации Вi событие A встречается также m раз, а событие 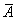происходит n-m раз, то вероятность каждой из таких комбинаций также равна 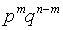. Итак

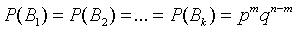
Все благоприятные комбинации являются, очевидно, несовместными. Поэтому (на основании аксиомы сложения вероятностей)

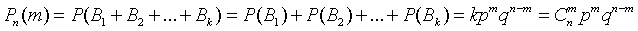
Следовательно,

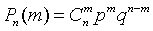
(13)

или, так как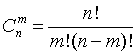

, то

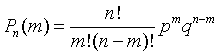
(13')

Формула (13) называется формулой Бернулли *.

Пример 1. Вероятность попадания в цель при одном выстреле равна 0,6. Какова вероятность того, что 8 выстрелов дадут 5 попаданий?

Решение: Здесь
n=8;
m=5;
p=0,6;
q=1-0,6=0,4.

Используя формулу (13'), имеем

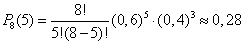
Часто необходимо знать, при каком значении m вероятность принимает наибольшее значение, т. е. требуется найти наивероятнейшее число 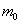наступления события A в данной серии опытов. Можно доказать, что число 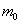должно удовлетворять двойному неравенству

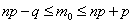
(14)

Заметим, что сегмент [np-q;np+p], в котором лежит 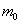, имеет длину (np+p)-(np-q)=p+q=1. Поэтому, если какой-либо из его концов не является целым числом, то между этими концами лежит единственное целое число, и 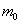определено однозначно. В том случае, если оба конца — целые числа, имеются два наивероятнейших значения: np-q и np+p.

Пример 2. Определить наивероятнейшее число попаданий в цель в примере 1.

Решение: Здесь
n=8;
p=0,6;
q=0,4;
np-q=8*0,6-0,4=4,4;
np+p=8*0,6+0,6=5,4.

Согласно формуле (14) наивероятнейшее значение 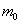лежит на сегменте [4.4;5.4] и, следовательно равно 5.

При больших значениях n подсчет вероятностей Pn(m) по формуле (13) связан с громоздкими вычислениями. В этом случае удобнее пользоваться следующей формулой:

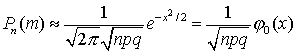
(15)

, где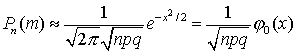

(p не равно нулю и единице), a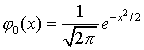

Формула (15) выражает так называемую локальную теорему Лапласа **. Точность этой формулы повышается с возрастанием n.

Функция 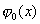, как мы увидим в дальнейшем, играет очень большую роль в теории вероятностей. Ее значения при различных значениях аргумента приведены в Приложении (см. табл. I).

Пример 3. Игральную кость бросают 80 раз. Определить вероятность того, что цифра 3 появится 20 раз.

Решение: Здесь
m=20;
n=80;
p=1/6;
q=1-1/6=5/6;

далее находим

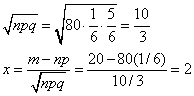
Используя формулу (15), получим

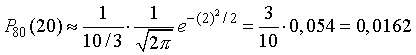
так как из табл. I находим, что

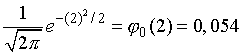
* Я. Бернулли (1654-1705) - швейцарский математик.
** П. Лаплас (1749—1827) — французский математик и астроном.