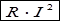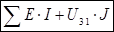ЗАДАЧА 1
1. Исходные данные
В формируемой схеме каждая ветвь содержит источник ЭДС (п.1.1) и резистивный элемент (п.1.3), а одна из ветвей - только источник тока (п.1.2), подключенный к зажимам a, b согласно коду {К}. Индексы в обозначениях ЭДС и сопротивлений означают номера зажимов ветви, в которую включен данный элемент. Кроме того, индексация в обозначениях ЭДС и тока источников, а также заданного тока в ветви с зажимами e, f (п.1.4) означает их направление от зажима, обозначенного в индексе первым, к другому зажиму.
1.1. ЭДС источников Ecd = E(5-c)(5-e)=50 В, E(5-c)(5-f)= E(5-f)(5-d)=
= E(5-d)(5-e)=30 В, Eef =?
1.2. Ток источника тока, подключенного к зажимам a, b, Jab = 0,9А.
1.3. Сопротивления в ветвях с источниками ЭДС Rcd = Rdf ==Rde = 80 Ом, Rce = Rcf = Ref =40 Ом.
1.4. Ток в элементе Ref Ief = 0,6 А.
2. Задание
1.Начертить схему согласно исходным данным, соединяя зажимы ветвей, пронумерованные одинаково, в один узел.
2.Произвести анализ схемы, определить число независимых уравнений Кирхгофа, составить и решить систему из этих уравнений.
3.Определить неизвестные токи и ЭДС, применив метод контурных токов.
4.Составить и рассчитать уравнение баланса мощностей.
5.Считая известными все ЭДС и ток источника тока, определить ток в элементе Rcd = R34 → I34 = ?, применив метод эквивалентного генератора. Попутно использовать методы узловых потенциалов и эквивалентных преобразований соединений резистивных элементов.
6. Считая известными все ЭДС и ток источника тока, определить ток в элементе Rcd = R34 → I34 = ?, применив метод узловых потенциалов в матричной форме.
7. Построить потенциальную диаграмму вдоль любого замкнутого контура.
3. Методические указания
3.1. При возникновении затруднений в составлении схемы по п.2.1 следует начертить каждую ветвь отдельно, пронумеровав ее зажимы, включить в нее элементы по п.1.1 -1.3, строго выдерживая направления ЭДС и токов по индексам обозначений. Пример формирования параметров и схемы приведен далее в п.4.1 задачи 2.
3.2. Анализ схемы при выполнении п.2.2 состоит в определении числа ветвей Nв , числа узлов Nу , числа независимых уравнений К1 , К2 , составленных по первому и второму законам Кирхгофа. Решения системы уравнений в п.2.2 не требуется. Пример выполнения п.2.2 задания содержится в п.4.2 задачи 2.
3.3. При выполнении п.2.3 объем вычислительной работы можно сократить, если выбрать контуры так, чтобы ветвь ef с заданным током Ief входила лишь в один контур. Контурные точки можно также определить, рассматривая ветвь с заданным током как ветвь с источником тока. После выполнения п.2.3 рекомендуется проверить результаты, подставив их в одно из уравнений, составленных в п.2.2 по второму закону Кирхгофа.
3.4. Перед выполнением п.2.5 следует произвести анализ схемы без ветви cd, т.е. определить число ветвей, узлов, независимых узловых уравнений. По найденным токам определяется ЭДС эквивалентного источника. Расчеты по п.2.5 не требуются.
Пример
Определение варианта к индивидуальному заданию
Шифр 807901
| П1 | А | Б | В | Г | Д | Е |
| К1 | ||||||
| П2 | А | Б | Д | Е | В | Г |
| К | ||||||
| П | a | b | c | d | e | f |
| Последняя цифра шифра | ||||||||||
| А | ||||||||||
| Б |
ЗАДАЧА 1
Исходные данные
В формируемой схеме каждая ветвь содержит источник ЭДС и резистивный элемент, а одна из ветвей - только источник тока, подключенный к зажимам a, b согласно коду {К}. Индексы в обозначениях ЭДС и сопротивлений означают номера зажимов ветви, в которую включен данный элемент. Кроме того, индексация в обозначениях ЭДС и тока источников, а также заданного тока в ветви с зажимами e, f означает их направление от зажима, обозначенного в индексе первым, к другому зажиму.
1. ЭДС источников Ecd = E(5-c)(5-e)= E34 = E24 = 50 В,
E(5-c)(5-f)= E(5-f)(5-d)= E(5-d)(5-e)= E23 = E31=E14 = 30 В, Eef = E12 = ?
2. Ток источника тока, подключенного к зажимам a, b, Jab = J13 = 0,9А.
3. Сопротивления в ветвях с источниками ЭДС
Rcd = Rd f =Rde = R34 = R42 =R41 = 80 Ом,
Rce = Rcf = Ref = R31 = R32 = R12 = 40 Ом.
4. Ток в элементе Ref = R12 Ief = I12 = 0,6 А.
ЗАДАНИЕ
1.Начертить схему согласно исходным данным, соединяя зажимы ветвей, пронумерованные одинаково, в один узел.
2.Произвести анализ схемы, определить число независимых уравнений Кирхгофа, составить и решить систему из этих уравнений.
3.Определить неизвестные токи и ЭДС, применив метод контурных токов.
4.Составить и рассчитать уравнение баланса мощностей.
5.Считая известными все ЭДС и ток источника тока, определить ток в элементе Rcd = R34 → I34 = ?, применив метод эквивалентного генератора. Попутно использовать методы узловых потенциалов и эквивалентных преобразований соединений резистивных элементов.
6. Считая известными все ЭДС и ток источника тока, определить ток в элементе Rcd = R34 → I34 = ?, применив метод узловых потенциалов в матричной форме.
7. Построить потенциальную диаграмму вдоль любого замкнутого контура.
РЕШЕНИЕ
Определение неизвестных токов и ЭДС с помощью законов Кирхгофа
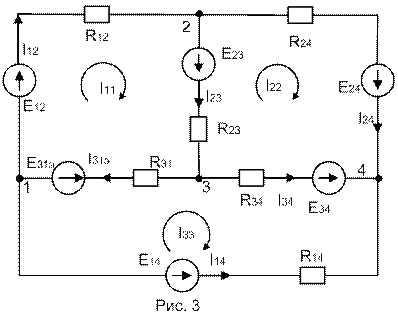
Согласно исходным данным составляем электрическую схему (Рис. 1). Произвольно выбираем направления токов в ветвях (кроме заданного направления тока I12).
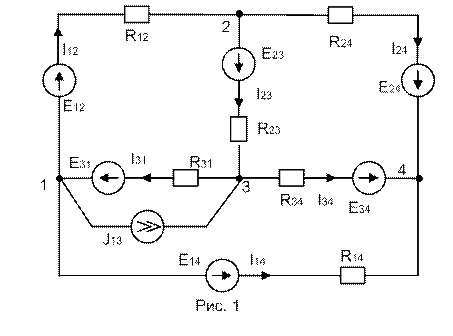
Составляем уравнения по правилам Кирхгофа.
По первому закону составим число уравнений равное числу узлов в схеме без единицы, т. е.: 4-1 = 3 уравнения:
узел 2: I12 = I23 +I24
узел 3: J13 +I23 = I31 + I34
узел 4: I14 + I24 +I34 = 0
По второму закону число уравнений равно числу ветвей схемы за вычетом уравнений, составленных по первому закону Кирхгофа и числу ветвей, содержащих источники токов, т.е. 7 – 4 + 1 - 1 = 3 (обход контуров производится по часовой стрелке):
I12 * R12 + I23 * R23 + I31 * R31 = E12 +E23 + E31
- I23 * R23 + I24 * R24 – I34 * R34 = - E23 + E24 – E34
- I31 * R31 + I34 * R34 – I14 * R14 = - E31 + E34 - E14
Объединим полученные системы в одну:
I12 = I23 +I24
J13 +I23 = I31 + I34
I14 + I24 +I34 = 0
I12 * R12 + I23 * R23 + I31 * R31 = E12 +E23 + E31
- I23 * R23 + I24 * R24 – I34 * R34 = - E23 + E24 – E34
- I31 * R31 + I34 * R34 – I14 * R14 = - E31 + E34 - E14
Подставляя в полученную систему уравнений заданные значения токов, величины ЭДС, источника тока и сопротивлений, получаем систему алгебраических уравнений с шестью неизвестными:
I23 + I24 = 0.6
I31 – I23 + I34 = 0.9
I14 + I24 +I34 = 0
40*I31 +40*I23 – E12 = 36
- 40*I23 + 80*I24 – 80* I34 = - 30
- 40*I31 – 80*I14 + 80*I34 = -10
Полученная система шести уравнений с шестью неизвестными имеет единственное решение. Для определения токов и ЭДС воспользуемся матричным методом решением системы алгебраических уравнений. Для этого представим данную систему в виде произведения матриц А*Х = В,решением которого будет уравнение Х = А-1*В. Результаты решения получаем используя табличный процессор EXCEL:
| ИСХОДНЫЕ МАТРИЦЫ | ||||||||||||
| I31 | I14 | I23 | I24 | I34 | E12 | |||||||
| I31 | 0,6 | |||||||||||
| -1 | I14 | 0,9 | ||||||||||
| A = | X= | I23 | B= | 0,0 | ||||||||
| -1 | I24 | 36,0 | ||||||||||
| -40 | -80 | I34 | -30,0 | |||||||||
| -40 | -80 | E12 | -10,0 | |||||||||
| Обратная матрица А | Результат | |||||||||||
| 0,667 | 0,762 | -0,476 | 0,000 | -0,002 | -0,006 | 0,6 | 1,217 | I31 | ||||
| -0,333 | -0,238 | 0,524 | 0,000 | -0,002 | -0,006 | 0,9 | -0,283 | I14 | ||||
| 0,667 | -0,095 | -0,190 | 0,000 | -0,006 | -0,002 | В= | 0,0 | 0,517 | I23 | |||
| 0,333 | 0,095 | 0,190 | 0,000 | 0,006 | 0,002 | 36,0 | 0,083 | I24 | ||||
| 0,000 | 0,143 | 0,286 | 0,000 | -0,004 | 0,004 | -30,0 | 0,200 | I34 | ||||
| 53,333 | 26,667 | -26,667 | -1,000 | -0,333 | -0,333 | -10,0 | 33,333 | E12 |
Определение неизвестных токов и ЭДС методом контурных токов
Так как узлы 1 и 3 соединены двумя ветвями, прибегнем к замене этих ветвей одной эквивалентной, определив E31Э (Рис.2).
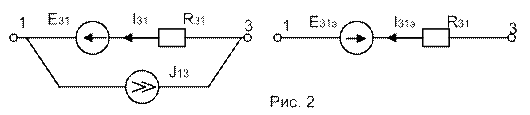
Величину эквивалентной ЭДС Е31Э определяем из разности потенциалов между узлами 3 и 1:
φ3 = φ1 + R31*(I31 + J) – E31;
U31 = φ3 - φ1 = R31*(I31 + J) – E31 = R31*I31 + R31 *J – E31 = R31*I31 + Е31Э .
Е31Э = R31 *J – E31 =40*0,9 – 30 = 6 В (т.е. ЭДС Е31Э имеет противоположное направление, как это показано в эквивалентной ветви).
I31 = I31Э + J.
Электрическая схема имеет следующий вид:
Для определения неизвестных величин методом контурных токов составляем основные уравнения для контуров:
 |
R11*I11 - R12*I22 - R13*I33 = E11
-R12*I11 + R22*I22 - R23*I33 = E22
-R13*I11 - R23*I22 + R33*I33 = E33
Применительно к заданной электрической схеме система имеет следующий вид:
(R12 + R23 + R31)*I11 – R23*I22 – R31*I33 = E12 + E23 – E31Э
-  R23*I11 + (R23 + R24 + R34)*I22 – R34* I33 = E24 – E23 – E34
R23*I11 + (R23 + R24 + R34)*I22 – R34* I33 = E24 – E23 – E34
- R31*I11 – R34*I22 + (R31 + R34 + R14)*I33 = E34 – E14 + E31Э
Подставим заданные значения сопротивлений, тока I11 = I12 и ЭДС, получим:
 |
- 40*I22 – 40*I33 – E12 = - 48
200*I22 – 80*I33 = - 6
-80*I22 + 200*I33 = 50
Аналогично предыдущему, используем матричный метод для решения этой системы:
| РЕШЕНИЕ ЗАДАЧИ МЕТОДОМ КОНТУРНЫХ ТОКОВ | ||||||||||||||
| I22 | I33 | E12 | ||||||||||||
| -40 | -40 | -1 | I22 | -48 | ||||||||||
| A = | -80 | X= | I33 | B= | -6 | |||||||||
| -80 | E12 | Результат | ||||||||||||
| 1,217 | I31 | |||||||||||||
| -0,283 | I14 | |||||||||||||
| Обратная матрица А | Результат | 0,517 | I23 | |||||||||||
| 0,006 | 0,002 | -48 | 0,083 | I22 | 0,083 | I24 | ||||||||
| 0,002 | 0,006 | B= | -6 | 0,283 | I33 | 0,200 | I34 | |||||||
| -1 | -0,333 | -0,333 | 33,333 | E12 | 33,333 | E12 | ||||||||
Токи в ветвях равны алгебраической сумме контурных токов:
I23 = I12 – I22; I34 = I33 – I12; I14 = - I33; I31Э = I12 – I33; I31 = I31Э + J.
Энергетический баланс электрической цепи
Баланс мощностей рассчитываем для схемы, изображенной на рис. 1, так как схема на рис. 3 не эквивалентна ей в отношении энергии.
Общий вид уравнения энергетического баланса:
ΣI2*R = ΣE*I + U31*J,
где U31 = φ3 – φ1 = I31*R31 – E31 = 18,667 В.
Расчет проведен в EXCEL:
| ЭНЕРГЕТИЧЕСКИЙ БАЛАНС ЭЛЕКТРИЧЕСКОЙ ЦЕПИ | |||||||||
| |||||||||
| R | E | E*I(J) | |||||||
| R31 | 59,211 | E31 | 30,000 | 36,5 | 1,217 | I31 | |||
| R14 | 6,422 | E14 | 30,000 | -8,5 | -0,283 | I14 | |||
| R23 | 10,678 | E23 | 30,000 | 15,5 | 0,517 | I23 | |||
| R24 | 0,556 | E24 | 50,000 | 4,1667 | 0,083 | I24 | |||
| R34 | 3,200 | E34 | 50,000 | 0,200 | I34 | ||||
| R12 | 14,400 | E12 | 33,330 | 19,998 | 0,600 | I12 | |||
| U31 | 18,667 | 16,8 | 0,9 | J | |||||
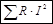
| 94,467 |
| 94,465 |
Таким образом, баланс мощностей рассчитан верно.
Расчет тока в ветви 3-4
Поскольку требуется определить ток лишь в одной из ветвей, целесообразно применить метод эквивалентного источника. Для этого вся остальная по отношению к выделенной ветви 3-4 часть цепи, содержащая источники и являющаяся активным двухполюсником, заменяется одним эквивалентным источником с элементами Еэ и Rэ . Согласно этому методу ЭДС Еэ равна напряжению U34x цепи с отключенной ветвью 3-4, а сопротивление Rэ равно сопротивлению цепи без ветви 3-4 относительно зажимов 3,4. Тогда формула для определения тока в ветви имеет следующий вид:
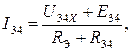 где U34X =φ3 – φ4 .
где U34X =φ3 – φ4 .
Схема принимает вид рис.4:
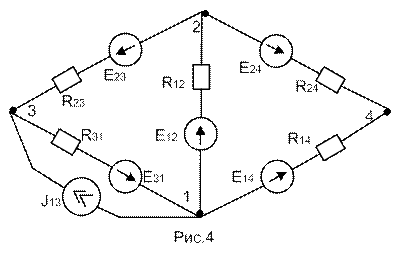
Для определения потенциалов точек 3 и 4 используем метод узловых потенциалов (φ1 = 0):
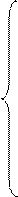
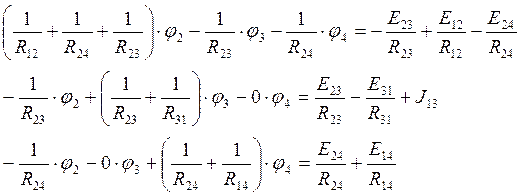
Подставляя числовые значения в полученную систему уравнений, получаем:
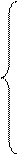
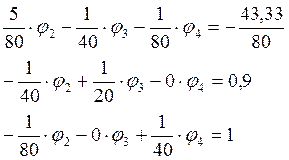
Решаем данную систему аналогично предыдущему в EXCEL:
| РЕШЕНИЕ МЕТОДОМ УЗЛОВЫХ ПОТЕНЦИАЛОВ | ||||||||
| 0,063 | -0,025 | -0,013 | φ2 | -0,541625 | ||||
| А= | -0,025 | 0,050 | 0,000 | X= | φ3 | B= | 0,9 | |
| -0,013 | 0,000 | 0,025 | φ4 | |||||
| Обратная матрица А | Результаты | |||||||
| 22,857 | 11,429 | 11,429 | 9,3343 | φ2 | ||||
| 11,429 | 25,714 | 5,714 | 22,667 | φ3 | ||||
| 11,429 | 5,714 | 45,714 | 44,667 | φ4 |
Находим напряжение холостого хода между узлами 3 и 4:
U34X = φ3 – φ4 =22.667 – 44.667 = -22 В.
Составляем схему для определения RЭ относительно зажимов 3 и 4 (рис.5):
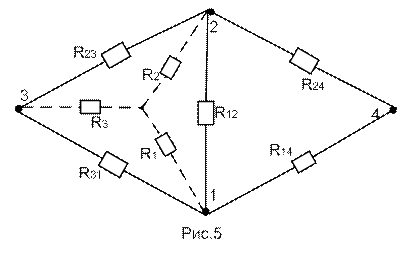
Преобразуем треугольник сопротивлений R12 = R23 = R31 = 40 Ом в звезду сопротивлений R1 = R2 = R3 = 40/3 Ом. Тогда эквивалентное сопротивление RЭ определяется по формуле:
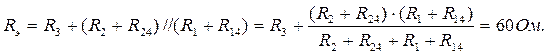
Определяем ток в ветви 3-4:
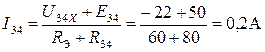 , величина которого равна ранее рассчитанному току другими методами.
, величина которого равна ранее рассчитанному току другими методами.
Дата добавления: 2014-12-06; просмотров: 1250;