Свободные колебания
Свободные колебания возникают в электрических цепях, содержащих катушку индуктивностью L, конденсатор емкостью С и сопротивление R, соединенные последовательно (рис. 1). Такая цепь называется колебательным контуром. Если предварительно зарядить конденсатор от источника постоянной эдс. (ключ в положении 1), а затем перевести ключ в положение 2, то конденсатор начнет разряжаться и в цепи потечет ток, создающий в катушке
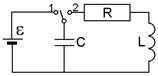 Рис. 1
Рис. 1
| индуктивности эдс самоиндукции, которая препятствуют нарастанию тока. Магнитное поле катушки растет, пока ток не достигнет максимума. При этом энергия электрического поля конденсатора, за исключением потерь на сопротивлении R, перейдет в энергию магнитного поля, а конденсатор разрядится. В этот момент ток начинает |
убывать, и эдс самоиндукции меняет знак, поддерживая убывающий ток. Конденсатор перезаряжается. Процесс заканчивается, когда заряд конденсатора достигнет максимального значения. В этот момент энергия магнитного поля катушки, за исключением потерь на сопротивлении R, перейдет в энергию электрического поля конденсатора, а ток в цепи прекратится. Затем процесс повторяется в обратном порядке, и в контуре возникают свободные колебания заряда, тока и напряжения на конденсаторе и индуктивности.
Пусть заряд на пластинах конденсатора в произвольный момент времени - q, напряжение на обкладках конденсатора - Uc, а ток в цепи - I. Согласно второму правилу Кирхгофа в произвольный момент времени
| I×R + Uc = ec, | (1) |
где ec – эдс самоиндукции.
Учитывая, что по определению сила тока I = 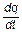 , эдс самоиндукции ec = - L×
, эдс самоиндукции ec = - L× 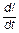 , а напряжение на обкладках конденсатора Uc =
, а напряжение на обкладках конденсатора Uc = 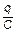 , выражение (1) можно представить в виде
, выражение (1) можно представить в виде
L× 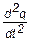 + R×
+ R× 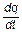 +
+ 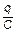 = 0
= 0
или
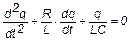
| (2) |
Полученное уравнение представляет собой дифференциальное уравнение затухающих колебаний, согласно которому на обкладках конденсатора происходит изменение заряда по закону
| q = q0×e-b×t×cos(wt + jo) | (3) |
c амплитудой A = q0×e-b×t, частотой 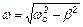 и начальной фазой jo, где q0 - начальный заряд конденсатора; b =
и начальной фазой jo, где q0 - начальный заряд конденсатора; b = 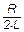 - коэффициент затухания – величина, характеризующая быстроту затухания амплитуды колебаний с течением времени;
- коэффициент затухания – величина, характеризующая быстроту затухания амплитуды колебаний с течением времени; 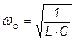 - частота собственных колебаний – частота колебаний, возникших бы в контуре при отсутствии сопротивления.
- частота собственных колебаний – частота колебаний, возникших бы в контуре при отсутствии сопротивления.
Из формулы (3) следует, что напряжение на пластинах конденсатора: меняется по закону
Uc = 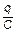 = Ucо×e-b×t×cos(wt + jo) = Ucо×e-b×t×cos(wt + jo)
| (4) |
где Ucо = 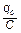 - напряжение на обкладках конденсатора в момент начала колебаний; Uса = Ucо×e-b×t – амплитуда напряжения на конденсаторе.
- напряжение на обкладках конденсатора в момент начала колебаний; Uса = Ucо×e-b×t – амплитуда напряжения на конденсаторе.
Изменение напряженияна конденсаторе Uc со временем приведено на
| рис. 2 (сплошная линия). Здесь же пунктиром показана зависимость амплитуды напряжения от времени. Быстрота затухания колебаний характеризуется логарифмическим декрементом затухания l – величиной, представляющей собой логарифм отношения двух последовательных амплитуд: | 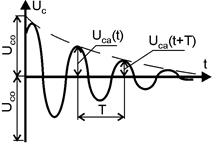 Рис. 2
Рис. 2
|
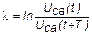 .
. 
Из определения логарифмического декремента затухания вытекает его связь с коэффициентом затухания в виде
l = b×T = 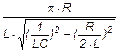 .
.
Тогда уменьшение амплитуды напряжения на конденсаторе в зависимости от числа колебаний можно представить в виде
Uса = Ucо×e - l×N,
где N - число колебаний.
В электротехнике и радиотехнике для характеристики качества контура используется понятие добротности контура
Q = 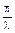 .
.
Очевидно, чем выше добротность контура Q, тем меньшеl и тем медленнее затухают колебания.
При малом затухании ( R ® 0) w » w0 , тогда
l » 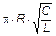 и Q =
и Q = 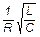 .
.
Дата добавления: 2014-12-06; просмотров: 968;
