Метод электрического моделирования

Определение потенциала в электростатическом поле экспериментально сложно, поэтому прибегают к моделированию электростатичес­кого поля электрическим полем в проводящей среде, измерения в ко­торой проще, чем в непроводящей. В данной работе электростатическое поле между электрода­ми моделируется полем стационарного элек­трического тока между электро­дами такой же формы. Правомерность такого моделирования обусловлена следующими соображениями.

Распределение электрического поля в пространстве определяется системой дифференциальных уравнений Максвелла в частных производных, решение которых зависит также от граничных условий. Если форма уравнений, описывающих поле стационарного тока и электростатическое, при одинаковых граничных условиях одинакова, то характеристики электрического поля в обоих случаях также одинаковы. Покажем, что форма уравнений при моделировании сохраняется.

Уравнения Максвелла для электростатического поля при отсутствии объемных электрических зарядов имеют вид

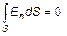	,	(3)
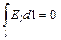	.	(4)

Уравнение (3) - не что иное, как теорема Гаусса, а уравнение (4) - условие потенциальности электростатического поля.

С другой стороны, для любой замкнутой поверхности в прост­ранстве между электродами, в котором течет стационарный ток плотностью j, можно записать по закону сохранения электрического заряда

,

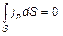(5)

т.е. количество зарядов, вошедших внутрь поверхности, равно коли­честву зарядов, вышедших из неё. Используя закон Ома в дифференциальной форме

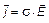
(6)

где s - проводимость среды, из уравнений (5) и (6) получаем

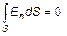
(7)

Кроме того, очевидно, что в отсутствие переменных магнитных полей для стационарного тока циркуляция вектора напряженности равна нулю

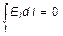
(8)

Уравнения (7) и (8) описывают поле стационарного тока между эле­ктродами данной формы. Уравнения (3) и (4) для электростатическо­го поля, (7) и (8) для поля стационарного тока полностью идентич­ны. Если проводимость среды между электродами намного меньше проводимости материала электродов, то поверхность последних является практически эквипотенциальной, как и в случаях электростатического поля, т.е. граничные условия также одинаковы.

Следует отметить, что уравнения, идентичные уравнениям (3) и (4), описывают также поле скоростей текущей жидкости и температурное поле, что позволяет решать задачи гидродинамики и теплопроводности методом электрического моделирования.