Решение системы с помощью обратной матрицы

Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.

Пример 11

Решить систему с матричным методом

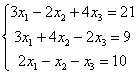
Решение: Запишем систему в матричной форме:
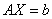, где

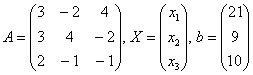
Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице 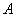нужно было бы поставить нули.

Решение системы найдем по формуле .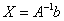

Я не буду приводить вывод этой формулы, так как его практически никогда не требуют в оформлении данной задачи. Согласно формуле нам нужно найти обратную матрицу 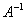и выполнить матричное умножение 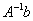. Алгоритм нахождения обратной матрицы подробно разобран на уроке Как найти обратную матрицу?

Обратную матрицу найдем по формуле:
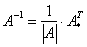, где 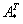– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

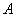Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.