Если в высшей математике Вы имеете дело с дробными числами, то все вычисления старайтесь проводить в обыкновенных правильных и неправильных дробях.

Именно 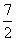, а не 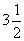или !

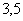Запятую можно использовать лишь иногда, в частности, если 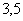– это окончательный ответ какой-нибудь задачи, и с этим числом больше не нужно выполнять никаких действий.

Многие читатели наверняка подумали «да зачем такое подробное объяснение, как для класса коррекции, и так всё понятно». Ничего подобного, вроде бы такой простой школьный пример, а сколько ОЧЕНЬ важных выводов! Вот еще один:

Любое задание следует стремиться выполнить самым рациональным способом.Хотя бы потому, что это экономит время и нервы, а также снижает вероятность допустить ошибку.

Если в задаче по высшей математике Вам встретилась система двух линейных уравнений с двумя неизвестными, то всегда можно использовать метод подстановки (если не указано, что систему нужно решить другим методом) Ни один преподаватель не снизит оценку за использование «школьного метода».
Более того, в ряде случаев метод подстановки целесообразно использовать и при большем количестве переменных.

Пример 2

Решить систему линейных уравнений с тремя неизвестными

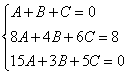
Похожая система уравнений часто возникает при использовании так называемого метода неопределенных коэффициентов, когда мы находим интеграл от дробно-рациональной функции. Рассматриваемая система взята мной как раз оттуда.

При нахождении интеграла – цель быстро найти значения коэффициентов 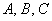, а не изощряться формулами Крамера, методом обратной матрицы и т.д. Поэтому, в данном случае уместен именно метод подстановки.

Когда дана любая система уравнений, в первую очередь желательно выяснить, а нельзя ли ее как-нибудь СРАЗУ упростить? Анализируя уравнения системы, замечаем, что второе уравнение системы можно разделить на 2, что мы и делаем:

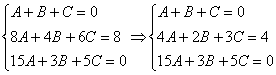
Справка: математический знак 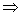обозначает «из этого следует это», он часто используется в ходе решения задач.

Теперь анализируем уравнения, нам нужно выразить какую-нибудь переменную через остальные. Какое уравнение выбрать? Наверное, Вы уже догадались, что проще всего для этой цели взять первое уравнение системы:

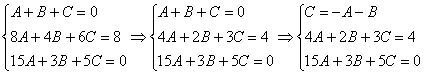
Здесь без разницы, какую переменную выражать, можно было с таким же успехом выразить 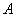или .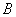

Далее, выражение для 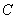подставляем во второе и третье уравнения системы:

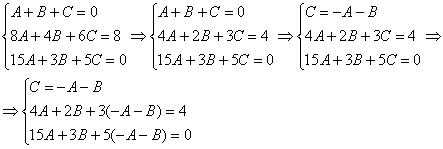
Раскрываем скобки и приводим подобные слагаемые:

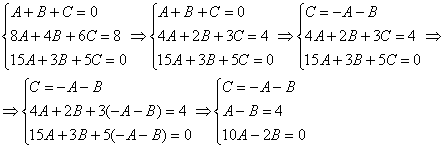
Третье уравнение делим на 2:

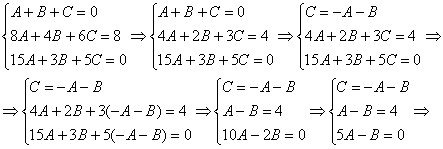
Из второго уравнения выразим 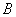и подставим в третьей уравнение:

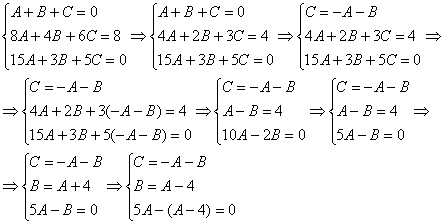
Практически всё готово, из третьего уравнения находим: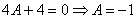
Из второго уравнения: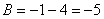
Из первого уравнения: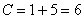

Ответ: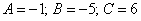

Проверка: Подставим найденные значения переменных в левую часть каждого уравнения системы:

1)
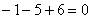
2)
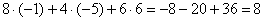
3)

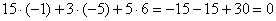
Получены соответствующие правые части уравнений, таким образом, решение найдено верно.

Пример 3

Решить систему линейных уравнений с 4 неизвестными

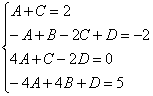
Это пример для самостоятельного решения (ответ в конце урока).