Решение системы по правилу Крамера

Представляю Вашему вниманию вторую часть урока Как решить систему линейных уравнений? В первой части мы рассмотрели немного теоретического материала, метод подстановки, а также метод почленного сложения уравнений системы. А сейчас мы разберём правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод).

Для того, чтобы освоить данный параграф Вы должны уметь раскрывать определители «два на два» и «три на три». Если с определителями плохо, пожалуйста, изучите урок Как вычислить определитель?

Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!

Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.

Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!

Рассмотрим систему уравнений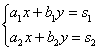

На первом шаге вычислим определитель 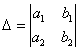, его называют главным определителем системы.

Если 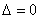, то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса.

Если 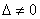, то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
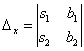и

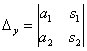
На практике вышеуказанные определители также могут обозначаться латинской буквой .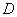

Корни уравнения находим по формулам:
,

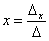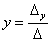
Пример 7

Решить систему линейных уравнений

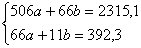
Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.

Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

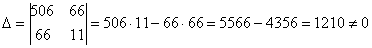, значит, система имеет единственное решение.

;

;

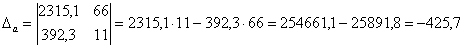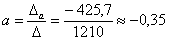
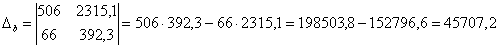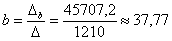
Ответ: ,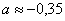

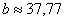
Как видите, корни получились иррациональными, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.

Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательнымфрагментом оформления задания является следующий фрагмент: « 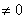, значит, система имеет единственное решение». В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.

Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения 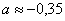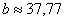в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.

Пример 8

Решить систему по формулам Крамера. Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

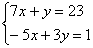
Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

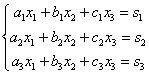
Находим главный определитель системы:

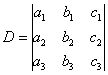
Если 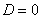, то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса.

Если 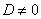, то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,

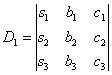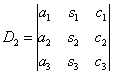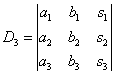
И, наконец, ответ рассчитывается по формулам:
, ,

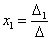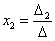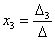
Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов 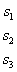последовательно «прогуливается» слева направо по столбцам главного определителя.

Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по такому же принципу.

Пример 9

Решить систему по формулам Крамера.

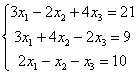
Решение: Решим систему по формулам Крамера.

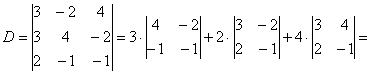
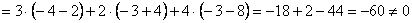, значит, система имеет единственное решение.

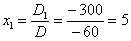
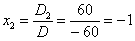
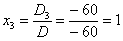
Ответ: .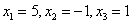

Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.

Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .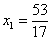
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:

1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие. Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).

2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде 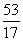. Как управляться с дробями, подробно расписано в ответе для Примера 8.

Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.

Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:

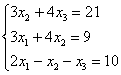
Здесь в первом уравнении отсутствует переменная 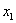, во втором – переменная 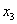. В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
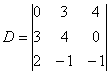– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).