Частные производные второго порядка функции трёх переменных
Общий принцип нахождения частных производных порядка второго порядка функции трёх переменных аналогичен принципу нахождения частных производных 2-го порядка функции двух переменных. Поэтому, если вы хорошо проработали урок Частные производные функции двух переменных, то будет всё очень просто.
Для того чтобы найти частные производные второго порядка, необходимо сначала найти частные производные первого порядка 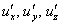 или в другой записи:
или в другой записи: 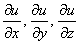 .
.
Частных производных второго порядка девять штук.
Первая группа – это вторые производные по тем же переменным:
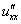 или
или 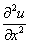 – вторая производная по «икс»;
– вторая производная по «икс»;
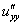 или
или 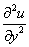 – вторая производная по «игрек»;
– вторая производная по «игрек»;
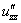 или
или 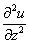 – вторая производная по «зет».
– вторая производная по «зет».
Вторая группа – это смешанные частные производные 2-го порядка, их шесть:
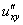 или
или 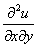 – смешанная производная «икс по игрек»;
– смешанная производная «икс по игрек»;
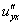 или
или 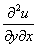 – смешанная производная «игрек по икс»;
– смешанная производная «игрек по икс»;
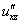 или
или 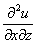 – смешанная производная «икс по зет»;
– смешанная производная «икс по зет»;
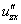 или
или 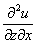 – смешанная производная «зет по икс»;
– смешанная производная «зет по икс»;
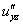 или
или 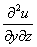 – смешанная производная «игрек по зет»;
– смешанная производная «игрек по зет»;
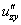 или
или 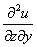 – смешанная производная «зет по игрек».
– смешанная производная «зет по игрек».
Как и для случая функции двух переменных, при решении задач можно ориентироваться на следующие равенства смешанных производных второго порядка:
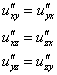
Примечание: строго говоря, это не всегда так
На всякий случай несколько примеров, как правильно читать сиё безобразие вслух:
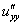 – «у два штриха дважды по игрек»;
– «у два штриха дважды по игрек»;
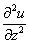 – «дэ два у по дэ зет квадрат»;
– «дэ два у по дэ зет квадрат»;
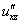 – «у два штриха по икс по зет»;
– «у два штриха по икс по зет»;
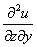 – «дэ два у по дэ зет по дэ игрек».
– «дэ два у по дэ зет по дэ игрек».
Примеры на нахождение частных производных 2-го прядка для функции трёх переменных на практике встречаются реже. Обычно они не очень сложные, но довольно большие по объему.
Пример 10
Найти все частные производные первого и второго порядка функции трёх переменных
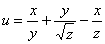
Решение: Сначала найдем частные производные первого порядка:
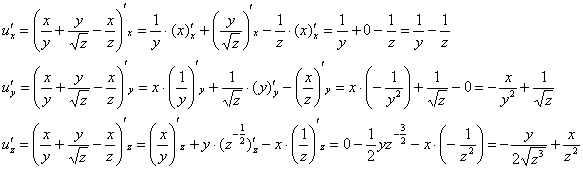
Частные производные второго порядка рекомендую начинать искать со смешанных производных, поскольку это позволит выяснить, а правильно ли вообще найдены производные первого порядка.
Берём найденную производную 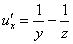 и дифференцируем её по «игрек»:
и дифференцируем её по «игрек»:
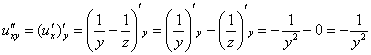
Берём найденную производную 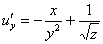 и дифференцируем её по «икс»:
и дифференцируем её по «икс»:
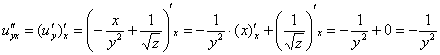
Равенство 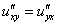 выполнено. Гуд.
выполнено. Гуд.
Разбираемся со второй парой смешанных производных.
Берём найденную производную 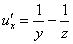 и дифференцируем её по «зет»:
и дифференцируем её по «зет»:
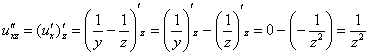
Берём найденную производную 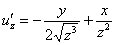 и дифференцируем её по «икс»:
и дифференцируем её по «икс»:
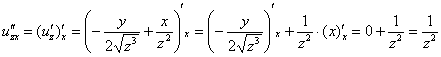
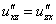 – всё путём.
– всё путём.
Аналогично разбираемся с третьей парой смешанных производных:
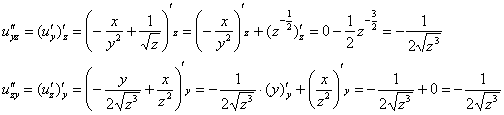
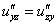 Нормалёк.
Нормалёк.
После проделанных трудов гарантированно можно утверждать, что, во-первых, мы правильно нашли все частные производные 1-го порядка, во-вторых, правильно нашли и смешанные частные производные 2-го порядка.
Осталось найти ещё три частные производные второго порядка, вот здесь уже во избежание ошибок следует максимально сконцентрировать внимание:
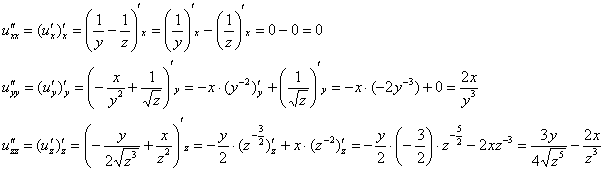
Готово. Повторюсь, задание не столько сложное, сколько объемное. Решение можно сократить и сослаться на равенства смешанных частных производных, но в этом случае не будет проверки. Поэтому лучше таки потратить время и найти все производные (к тому же это может потребовать преподаватель), или, в крайнем случае, выполнить проверку на черновике.
Пример 11
Найти все частные производные первого и второго порядка функции трёх переменных
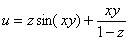
Это пример для самостоятельного решения.
Решения и ответы:
Пример 2:Решение:
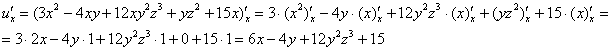
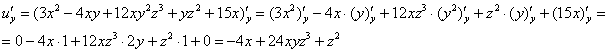
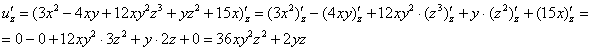
Пример 4:Решение:Найдем частные производные первого порядка.
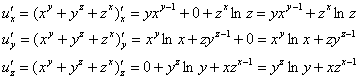
Составим полный дифференциал первого порядка:
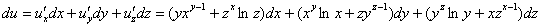
Пример 6:Решение:Вычислим частные производные первого порядка в точке 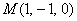 :
:

Пример 7:Решение:Вычислим частные производные первого порядка в точке 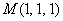 :
:
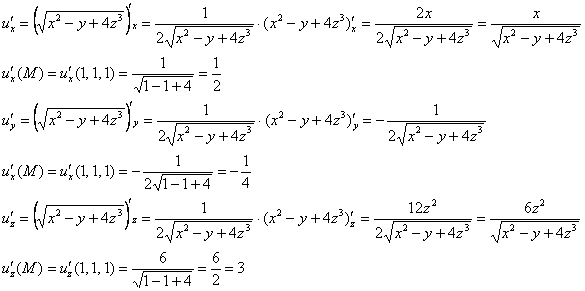
Пример 9:Решение:Найдем частные производные первого порядка:
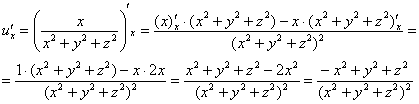
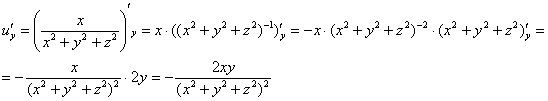
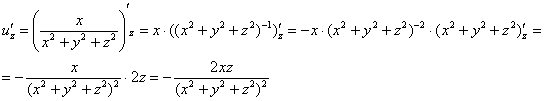
Пример 11:Решение:Найдем частные производные первого порядка:
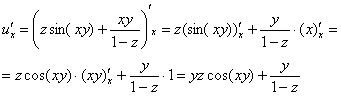
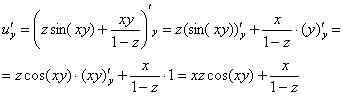
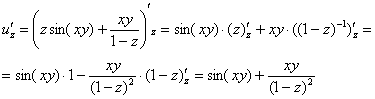
Найдем частные производные второго порядка:
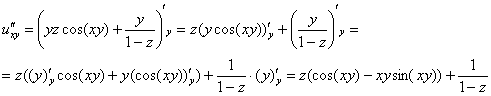
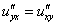
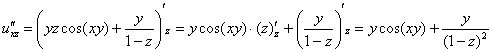
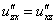
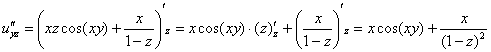
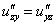
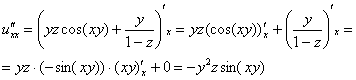
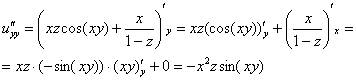
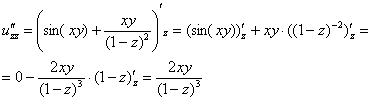
Дата добавления: 2014-11-29; просмотров: 3549;
