Приближенные вычисления с помощью полного дифференциала функции двух переменных
Всё будет очень и очень похоже, поэтому, если вы зашли на эту страницу именно этим заданием, то сначала рекомендую просмотреть хотя бы пару примеров предыдущего пункта.
Для изучения параграфа необходимо уметь находить частные производные второго порядка, куда ж без них. На вышеупомянутом уроке функцию двух переменных я обозначал через букву 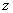 . Применительно к рассматриваемому заданию удобнее использовать эквивалентное обозначение
. Применительно к рассматриваемому заданию удобнее использовать эквивалентное обозначение 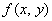 .
.
Как и для случая функции одной переменной, условие задачи может быть сформулировано по-разному, и я постараюсь рассмотреть все встречающиеся формулировки.
Пример 8
Вычислить приближенное значение функции 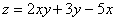 в точке
в точке 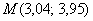 с помощью полного дифференциала, оценить абсолютную и относительную погрешность.
с помощью полного дифференциала, оценить абсолютную и относительную погрешность.
Решение:Как бы ни было записано условие, в самом решении для обозначения функции, повторюсь, лучше использовать не букву «зет», а 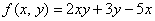 .
.
А вот и рабочая формула:
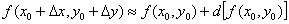
Перед нами фактически старшая сестра формулы 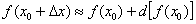 предыдущего параграфа. Переменная только прибавилась. Да что говорить, сам алгоритм решения будет принципиально таким же!
предыдущего параграфа. Переменная только прибавилась. Да что говорить, сам алгоритм решения будет принципиально таким же!
По условию требуется найти приближенное значение функции в точке 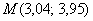 .
.
Число 3,04 представим в виде 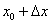 . Колобок сам просится, чтобы его съели:
. Колобок сам просится, чтобы его съели:
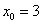 ,
, 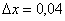
Число 3,95 представим в виде 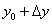 . Дошла очередь и до второй половины Колобка:
. Дошла очередь и до второй половины Колобка:
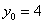 ,
, 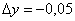
И не смотрите на всякие лисьи хитрости, Колобок есть – надо его съесть.
Вычислим значение функции в точке 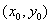 :
:
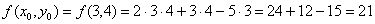
Дифференциал функции в точке 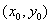 найдём по формуле:
найдём по формуле:
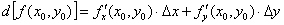
Из формулы следует, что нужно найти частные производные первого порядка и вычислить их значения в точке 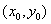 .
.
Вычислим частные производные первого порядка в точке 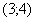 :
:
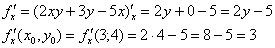
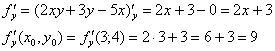
Полный дифференциал в точке 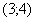 :
:
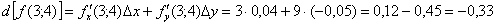
Таким образом, по формуле 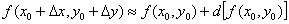 приближенное значение функции в точке
приближенное значение функции в точке 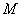 :
:
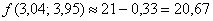
Вычислим точное значение функции в точке 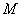 :
:
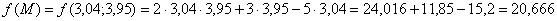
Вот это значение является абсолютно точным.
Погрешности рассчитываются по стандартным формулам, о которых уже шла речь в этой статье.
Абсолютная погрешность:
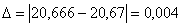
Относительная погрешность:
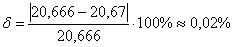
Ответ: 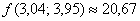 , абсолютная погрешность:
, абсолютная погрешность: 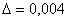 , относительная погрешность:
, относительная погрешность: 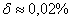
Пример 9
Вычислить приближенное значение функции 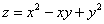 в точке
в точке 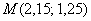 с помощью полного дифференциала, оценить абсолютную и относительную погрешность.
с помощью полного дифференциала, оценить абсолютную и относительную погрешность.
Это пример для самостоятельного решения. Кто остановится подробнее на данном примере, тот обратит внимание на то, что погрешности вычислений получились весьма и весьма заметными. Это произошло по следующей причине: в предложенной задаче достаточно велики приращения аргументов: 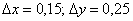 . Общая закономерность такова – чем больше эти приращения по абсолютной величине, тем ниже точность вычислений. Так, например, для похожей точки
. Общая закономерность такова – чем больше эти приращения по абсолютной величине, тем ниже точность вычислений. Так, например, для похожей точки 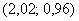 приращения будут небольшими:
приращения будут небольшими: 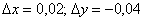 , и точность приближенных вычислений получится очень высокой.
, и точность приближенных вычислений получится очень высокой.
Данная особенность справедлива и для случая функции одной переменной (первая часть урока).
Пример 10
С помощью полного дифференциала функции двух переменных вычислить приближенно значение данного выражения. Вычислить это же выражение с помощью микрокалькулятора. Оценить в процентах относительную погрешность вычислений.
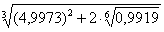
Решение: Вычислим данное выражение приближенно с помощью полного дифференциала функции двух переменных:
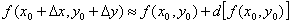
Отличие от Примеров 8-9 состоит в том, что нам сначала необходимо составить функцию двух переменных: 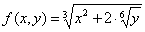 . Как составлена функция, думаю, всем интуитивно понятно.
. Как составлена функция, думаю, всем интуитивно понятно.
Значение 4,9973 близко к «пятерке», поэтому: 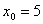 ,
, 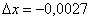 .
.
Значение 0,9919 близко к «единице», следовательно, полагаем: 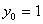 ,
, 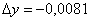 .
.
Вычислим значение функции в точке 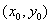 :
:
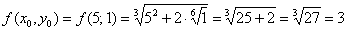
Дифференциал в точке 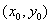 найдем по формуле:
найдем по формуле:
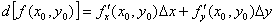
Для этого вычислим частные производные первого порядка в точке 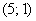 .
.
Производные здесь не самые простые, и следует быть аккуратным:
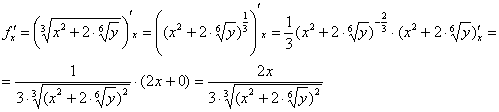 ;
;
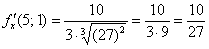
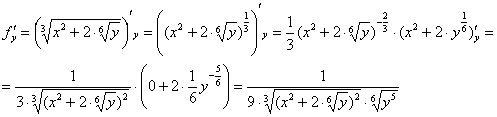
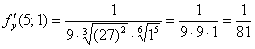 .
.
Полный дифференциал в точке 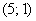 :
:
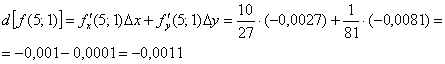
Таким образом, приближенное значение данного выражения:
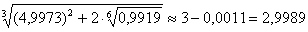
Вычислим более точное значение с помощью микрокалькулятора: 2,998899527
Найдем относительную погрешность вычислений:
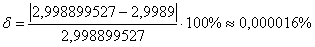
Ответ: 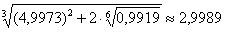 ,
, 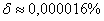
Как раз иллюстрация вышесказанному, в рассмотренной задаче приращения аргументов очень малы 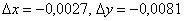 , и погрешность получилась фантастически мизерной.
, и погрешность получилась фантастически мизерной.
Пример 11
С помощью полного дифференциала функции двух переменных вычислить приближенно значение данного выражения. Вычислить это же выражение с помощью микрокалькулятора. Оценить в процентах относительную погрешность вычислений.
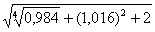
Это пример для самостоятельного решения. Примерный образец чистового оформления в конце урока.
Как уже отмечалось, наиболее частный гость в данном типе заданий – это какие-нибудь корни. Но время от времени встречаются и другие функции. И заключительный простой пример для релаксации:
Пример 12
С помощью полного дифференциала функции двух переменных вычислить приближенно значение функции 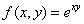 , если
, если 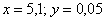
Решение ближе к дну страницы. Еще раз обратите внимание на формулировки заданий урока, в различных примерах на практике формулировки могут быть разными, но это принципиально не меняет сути и алгоритма решения.
Задачи вычислительной математики обычно не очень сложны, не очень интересны. Здесь самое важное - не допустить ошибку в обычных расчётах.
Решения и ответы:
Пример 2:Решение:Используем формулу: 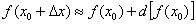
В данном случае: 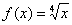 ,
, 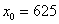 ,
, 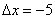
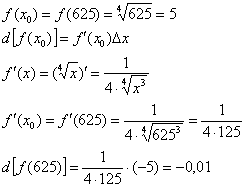
Таким образом: 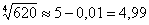
Ответ: 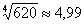
Пример 4:Решение:Используем формулу: 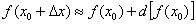
В данном случае: 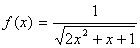 ,
, 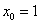 ,
, 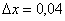
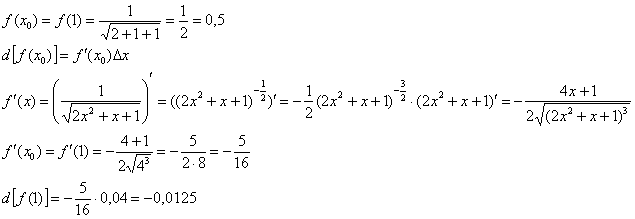
Таким образом: 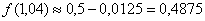
Вычислим более точное значение функции с помощью микрокалькулятора:
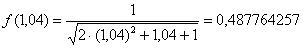
Абсолютная погрешность:
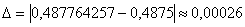
Относительная погрешность:
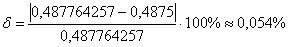
Ответ: 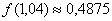 , абсолютная погрешность вычислений
, абсолютная погрешность вычислений 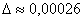 , относительная погрешность вычислений
, относительная погрешность вычислений 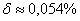
Пример 5:Решение:Используем формулу: 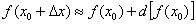
В данном случае: 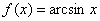 ,
, 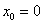 ,
, 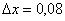
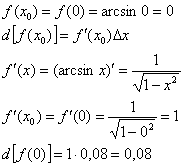
Таким образом: 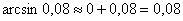
Ответ: 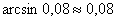
Пример 7:Решение:Используем формулу: 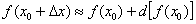
В данном случае: 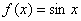 ,
, 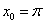 ,
, 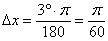
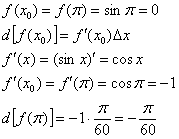
Таким образом: 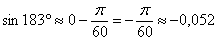
Ответ: 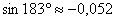
Пример 9:Решение: Используем формулу: 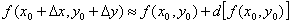
В данной задаче:
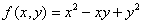 ,
, 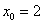 ,
, 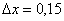 ,
, 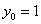 ,
, 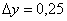 .
.
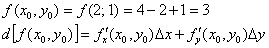
Вычислим частные производные первого порядка в точке 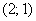 :
:
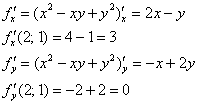
Полный дифференциал в точке 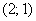 :
:
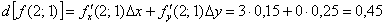
Таким образом: 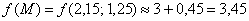
С помощью калькулятора вычислим точное значение функции в данной точке:
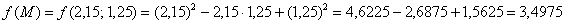
Абсолютная погрешность:
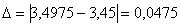
Относительная погрешность:
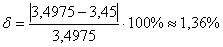
Ответ: 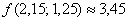 , абсолютная погрешность:
, абсолютная погрешность: 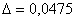 , относительная погрешность:
, относительная погрешность: 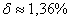
Пример 11:Решение: С помощью полного дифференциала вычислим данное выражение приближенно:
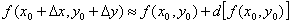
В данной задаче:
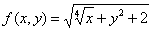
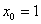 ,
, 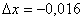
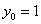 ,
, 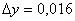
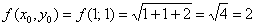
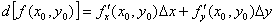
Вычислим частные производные первого порядка в точке 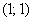 :
:
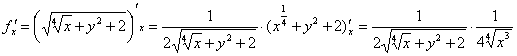
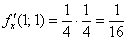
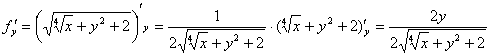
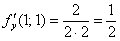
Полный дифференциал в точке 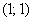 :
:
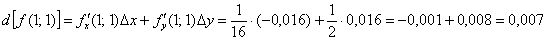
Таким образом, приближенное значение данного выражения:
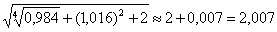
Значение, вычисленное с помощью микрокалькулятора: 2,007045533
Найдем относительную погрешность вычислений:
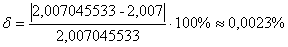
Ответ: 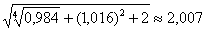 ,
, 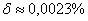
Пример 12: Решение:Используем формулу: 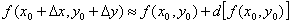 .
.
В данной задаче: 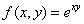 ,
, 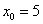 ,
, 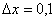 ,
, 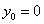 ,
, 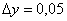 .
.
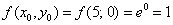
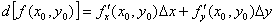
Вычислим частные производные первого порядка в точке 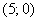 :
:
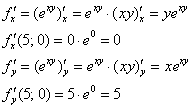
Полный дифференциал в точке 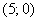 :
:
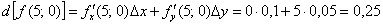
Таким образом:
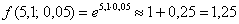
Ответ: 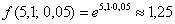
Дата добавления: 2014-11-29; просмотров: 3491;
