Приближенные вычисления с помощью дифференциала функции одной переменной

В первом параграфе рулит функция одной переменной. Как все знают, она обозначается через 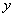или через 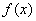. Для данной задачи намного удобнее использовать второе обозначение. Сразу перейдем к популярному примеру, который часто встречается на практике:

Пример 1

Вычислить приближенно 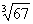, заменяя приращения функции ее дифференциалом.

Решение: Пожалуйста, перепишите в тетрадь рабочую формулу для приближенного вычисления с помощью дифференциала:

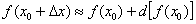
Начинаем разбираться, здесь всё просто!

На первом этапе необходимо составить функцию 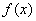. По условию предложено вычислить кубический корень из числа: 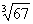, поэтому соответствующая функция имеет вид: 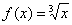. Нам нужно с помощью формулы найти приближенное значение .

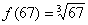Смотрим на левую часть формулы 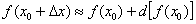, и в голову приходит мысль, что число 67 необходимо представить в виде 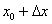. Как проще всего это сделать? Рекомендую следующий алгоритм: вычислим данное значение на калькуляторе:
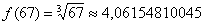– получилось 4 с хвостиком, это важный ориентир для решения.

В качестве 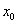подбираем «хорошее» значение, чтобы корень извлекался нацело. Естественно, это значение 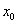должно быть как можно ближек 67. В данном случае: 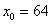. Действительно: .

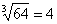Примечание: Когда с подбором 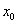всё равно возникает затруднение, просто посмотрите на скалькулированное значение (в данном случае 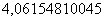), возьмите ближайшую целую часть (в данном случае 4) и возведите её нужную в степень (в данном случае 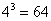). В результате и будет выполнен нужный подбор .

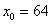Если 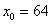, то приращение аргумента: .

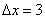Итак, число 67 представлено в виде суммы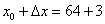

Далее работаем с правой частью формулы .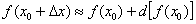

Сначала вычислим значение функции в точке 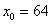. Собственно, это уже сделано ранее:

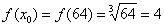
Дифференциал в точке находится по формуле:
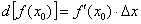– тоже можете переписать к себе в тетрадь.

Из формулы следует, что нужно взять первую производную:

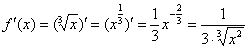
И найти её значение в точке :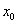

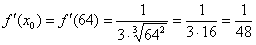
Таким образом:

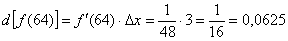
Всё готово! Согласно формуле :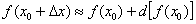

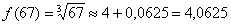
Найденное приближенное значение достаточно близко к значению 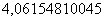, вычисленному с помощью микрокалькулятора.

Ответ: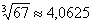

Пример 2

Вычислить приближенно 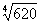, заменяя приращения функции ее дифференциалом.

Это пример для самостоятельного решения. Примерный образец чистового оформления и ответ в конце урока. Начинающим сначала рекомендую вычислить точное значение 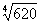на микрокалькуляторе, чтобы выяснить, какое число принять за 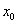, а какое – за 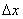. Следует отметить, что 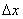в данном примере будет отрицательным.

У некоторых, возможно, возник вопрос, зачем нужна эта задача, если можно всё спокойно и более точно подсчитать на калькуляторе? Согласен, задача глупая и наивная. Но попытаюсь немного её оправдать. Во-первых, задание иллюстрирует смысл дифференциала функции. Во-вторых, в древние времена, калькулятор был чем-то вроде личного вертолета в наше время. Сам видел, как из местного политехнического института году где-то в 1985-86 выбросили компьютер размером с комнату (со всего города сбежались радиолюбители с отвертками, и через пару часов от агрегата остался только корпус). Антиквариат водился и у нас на физмате, правда, размером поменьше – где-то с парту. Вот так вот и мучились наши предки с методами приближенных вычислений. Конная повозка – тоже транспорт.

Так или иначе, задача осталась в стандартном курсе высшей математики, и решать её придётся. Это основной ответ на ваш вопрос =).

Пример 3

Вычислить приближенно с помощью дифференциала значение функции 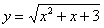в точке 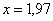. Вычислить более точное значение функции в точке 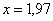с помощью микрокалькулятора, оценить абсолютную и относительную погрешность вычислений.

Фактически то же самое задание, его запросто можно переформулировать так: «Вычислить приближенное значение 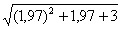с помощью дифференциала»

Решение: Используем знакомую формулу: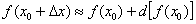
В данном случае уже дана готовая функция: 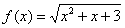. Ещё раз обращаю внимание, что для обозначения функции вместо «игрека» удобнее использовать .

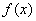Значение 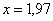необходимо представить в виде 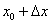. Ну, тут легче, мы видим, что число 1,97 очень близко к «двойке», поэтому напрашивается 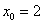. И, следовательно: .
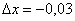Вычислим значение функции в точке :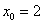

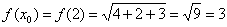
Используя формулу 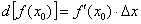, вычислим дифференциал в этой же точке.

Находим первую производную:

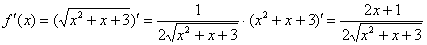
И её значение в точке :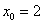

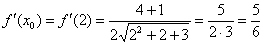
Таким образом, дифференциал в точке:

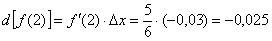
В результате, по формуле :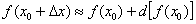

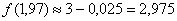
Вторая часть задания состоит в том, чтобы найти абсолютную и относительную погрешность вычислений.