Указания к выполнению работы. При решении прикладных задач вероятностные характеристики соответствующих случайных величин чаще всего неизвестны и должны определяться по экспериментальным
При решении прикладных задач вероятностные характеристики соответствующих случайных величин чаще всего неизвестны и должны определяться по экспериментальным данным. Такое статистическое описание результатов наблюдений, построение и проверка различных математических моделей, использующих понятие вероятности, составляют основное содержание математической статистики. Фундаментальными понятиями статистической теории являются понятия генеральной совокупности и выборки. Выборка – это конечный набор значений случайной величины, полученный в результате наблюдений. Число элементов выборки называется ее объемом. Если, например, y1, y2,…yN – наблюдаемые значения случайной величины Y, то объем данной выборки равен N.
Для выявления существования свойств неслучайных закономерностей, присущих данной совокупности, рассмотрим методы точечного и интервального оценивания основных характеристик случайных величин – среднего значения, дисперсии, функции плотности вероятности и др.
1. По условию задания выбранного варианта составляем выборку, включающую до 50 значений выходной величины y.
Например, по условию выбранного варианта задания, исследуется зависимость удельной работы резания К, Дж/см3 от толщины стружки а,мм и угла встречи jв, град., при продольно-торцовом фрезеровании сосны. Условия резания: влажность W=12%, высота срезаемого слоя Н=3 мм, угол резания d=60°, скорость резания V=40 м/c, радиус закругления лезвия r=5мкм. Принятый диапазон изменения факторов аср, 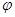 в и результаты эксперимента–значения выходной величины К в ПФЭ2К приведены в табл. 2.1
в и результаты эксперимента–значения выходной величины К в ПФЭ2К приведены в табл. 2.1
Таблица 2.1
Рабочая матрица плана ПФЭ 2К, к=2
| Номер опыта | Натуральные значения факторов | Значение выходной величины К, Дж/см3 | |
| а ср, мм | j b  , град , град
| ||
| а ср min=0,2 а ср max=0,6 а ср min=0,2 а ср max=0,6 | j b min =40 j b min=40 j b max=60 j b max=60 | К1= y1=32 К2= y2=19 К3= y3=38 К4= y4=23 |
Результаты экспериментов представляются, как правило, в виде случайных величин, характеризующих исследуемое свойство. Случайной величиной называют такую величину, значения которой изменяются при повторении опытов некоторым заранее не предсказуемым образом. В отличие от детерминированных величин, для случайной величины нельзя заранее точно сказать, какое конкретное значение она примет в определенных условиях, а можно только указать закон ее распределения. Закон распределения считается заданным, если указано множество значений случайной величины и указан способ количественного определения вероятности попадания случайной величины в любую область множества возможных значений.
Для того, чтобы получить множество значений, например, величины y3, (табл.2.1) нужно многократно повторить опыт 3.Однако организовать проведение физического эксперимента в условиях проведения учебного процесса затруднительно. Учитывая это обстоятельство, данные результатов опытов при выполнении лабораторных работ получают из уже существующих зависимостей при исследовании процессов (объектов) деревообработки.
Для составления выборки, на основе которой выполняются расчеты статистических характеристик в работе, используют значение выходной величины в одном любом опыте эксперимента (табл.2.1). Пусть это будет значение удельной работы резания в третьем опыте К3= y3=38 Дж/см3.Для получения выборки объемом 50 наблюдений, необходимо опыт со значениями факторов а ср =0,2 мм, j b =60° повторить пятьдесят раз. Для этого проводится имитационный эксперимент в соответствии с выражением [2, форм. 3.1].
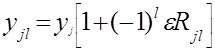 , (2.1)
, (2.1)
где yJℓ – значение выходного параметра в j-той серии и l-м дублированном опыте имитационного эксперимента, 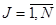 ,
, 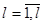 ;
;
yJ – значение выходной величины в исследовательском эксперименте,
yJ= y3=38 Дж/см3 (табл. 2.1);
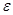 – относительная погрешность наблюдений, для процессов деревооб-
– относительная погрешность наблюдений, для процессов деревооб-
работки 
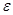 =0,01…0,10;
=0,01…0,10;
R – число в таблице случайных чисел, находящееся на J-той строке ( номер серии j опыта) в l-м столбце (номер дублированного опыта).
Значения RJl выбираются по табл. П.2 (Приложения) случайных чисел в виде блока чисел N´l=5´10, взятых наугад в любой ее части. Количество случайных чисел составит Nl=5´10=50. Их можно набрать с помощью генератора случайных чисел на компьютере или калькуляторе.
Заполняется таблица случайных чисел по образцу табл. 2.2.
Таблица 2.2
Таблица случайных чисел RJl
| Номер строки, J (табл.П.2) | Номер столбца, l | |||||||||
Случайные значения yJL в имитационном эксперименте достигаются изменением значения относительной погрешности 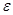 и случайностью числа RJl. Подставляя их в выражение (2.1), будем получать случайные значения yJℓ, например: y11=38[1+(-1)10,01´1]=37,6;
и случайностью числа RJl. Подставляя их в выражение (2.1), будем получать случайные значения yJℓ, например: y11=38[1+(-1)10,01´1]=37,6;
y22=38[1+(-1)20,02´0]=38,0;
y5,10=38[1+(-1)100,01´7]=40,6.
Условия эксперимента и результаты расчетов удельной работы резания по выражению (2.1) занесем в табл. 2.3.
Таблица 2.3
Результаты имитационного эксперимента
| Номер строки (серии) J | Погрешность, E | Значение удельной работы резания К3=y3 для числа RJl (табл.2.2) | |||||||||
| Номер столбца, l | |||||||||||
| 0,01 | 37,6 | 38,8 | 41,0 | 38,0 | 35,3 | 34,6 | 34,6 | 34,6 | 35,4 | 38,0 | |
| 0,02 | 44,1 | 38,0 | 31,2 | 34,2 | 31,2 | 38,0 | 31,2 | 37,2 | 37,2 | 32,7 | |
| 0,01 | 38,8 | 38,0 | 40,3 | 36,7 | 40,3 | 37,7 | 38,0 | 39,5 | 38,0 | 38,8 | |
| 0,02 | 37,2 | 34,2 | 31,2 | 34,2 | 38,7 | 35,7 | 41,0 | 32,7 | 42,1 | 41,0 | |
| 0,01 | 41,0 | 40,3 | 34,6 | 40,3 | 34,6 | 39,5 | 36,7 | 34,6 | 40,6 |
По результатам имитационного эксперимента сформирована выборка (в табл. 2.3 выделена прямоугольником) объемом из 50 наблюдений (К=j ( 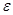 J, RJl)). Выбор значения относительной погрешности
J, RJl)). Выбор значения относительной погрешности 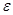 для имитационных экспериментов рекомендуется ограничить величиной
для имитационных экспериментов рекомендуется ограничить величиной 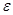 £ 0,03.
£ 0,03.
3. Построение вариационного ряда. Вариационный ряд y1, y2, …, yN получают путем расположения yi (i=1,2,…,N) в порядке возрастания от ymin до ymax так, чтобы ymin= y1£ y2£ y3£… £ yN= ymax. Выборке (табл. 2.3) соответствует вариативный ряд:
| 31,2 | 31,2 | 81,2 | 31,2 | 32,7 | 32,7 | 34,2 | 34,2 | 34,2 | 34,6 | |
| 34,6 | 34,6 | 34,6 | 34,6 | 34,6 | 35,3 | 35,4 | 35,4 | 35,7 | 35,7 | |
| 36,7 | 36,7 | 37,2 | 37,2 | 37,2 | 37,6 | 37,6 | 38,0 | 38,0 | 38,0 | |
| 38,0 | 38,0 | 38,0 | 38,0 | 38,8 | 38,8 | 38,8 | 39,5 | 39,5 | 40,3 | |
| 40,3 | 40,3 | 40,6 | 41,0 | 41,0 | 41,0 | 41,0 | 41,0 | 42,6 | 44,1 |
Вариационный (статистический) ряд разбивают на интервалы (кванты), число которых R вычисляют по формуле [4]
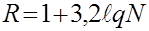 , (2.2)
, (2.2)
где N – объем выборки, N=50.
По формуле (2.2) R будет равно: R=1+3,2lq 50=6,4.
Расчетное значение числа интервалов округляют до ближайшего целого нечетного числа, R=7.
Определяют длину интервала по формуле
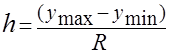 , (2.3)
, (2.3)
или 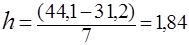 .
.
Округляют длину интервала, h=2,0. Границы интервалов определяют из выражения
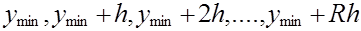 . (2.4)
. (2.4)
Середины интервалов y*i(i=1. 2 …R) определяют как полусумму границ интервалов
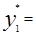
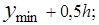
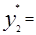
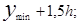
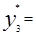
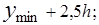 ….;
….; 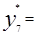
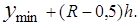 (2.5)
(2.5)
Расположение квантов на числовой оси выполняют следующим образом. Определяют середину области изменения выборки (центр распределения yц) по формуле
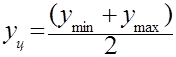 (2.6)
(2.6)
и принимают за центр некоторого интервала. В нашем случае yц совмещают с серединой четвертого интервала, которая размещается согласно формулы (2.6) в точке с координатой yц.
yц = (31,2 + 44,1)/2 =37,65.
После этого легко определяются границы и окончательное количество указанных интервалов. Интервалы симметрично располагаются относительно 4-го интервала по схеме на рисунке 2.1.
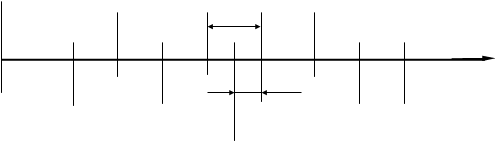 32,65 36,65 40,65
32,65 36,65 40,65
h=2
0 h/2 y, мм
ymin=30,65 34,65 38,65 42,65 ymax=44,65
yц=37,65
Рис. 2.1. Схема размещения квантов на числовой оси
В совокупности кванты должны перекрывать всю область изменения выборки от ymin до ymax (от 31,2 до 44,1 Дж/см3). При расчете границ интервалов и их середины за ymin принимается значение 30,65.
Далее подсчитывают количество наблюдений mJ, попавших в каждый квант: mJ равно числу членов вариационного ряда, для которых справедливо неравенство
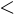
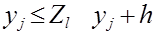 , (2.7)
, (2.7)
где yJ и yJ + h границы J-го интервала.
Значение Zl, попавшее на границу между (J-1) и J-м интервалами, относят к J-ому интервалу.
4. Для вычисления основных характеристик случайных величин строют вспомогательную таблицу по образцу табл. 2.4.
Таблица 2.4
Значения удельной работы резания К=y3
по результатам эксперимента
   Номер интервала, J Номер интервала, J
| Границы интервала, Дж/см3 | Середина интервала y*J, Дж/см3 | Число наблюдений в интервале, mJ | Относительная частота, P*J = mJ/N | y*J mJ | y*J - y | (y*J – y)2 | mJ (y*J – y)2 |
| 30,65-32,65 | 31,65 | 0,08 | 126,6 | - 6,65 | 44,2 | 176,9 | ||
| 32,65-34,65 | 33,65 | 0,22 | 370,2 | - 4,65 | 21,6 | 237,8 | ||
| 34,65-36,65 | 35,65 | 0,12 | 213,9 | - 2,65 | 7,0 | 42,0 | ||
| 36,65-38,65 | 37,65 | 0,28 | 527,1 | 0,65 | 0,4 | 5,9 | ||
| 38,65-40,65 | 39,65 | 0,16 | 317,2 | 2,65 | 7,0 | 56,0 | ||
| 40,65-42,65 | 41,65 | 0,12 | 249,9 | 4,65 | 21,6 | 129,6 | ||
| 42,65-44,65 | 43,65 | 0,02 | 437,0 | 6,65 | 44,2 | 44,2 |
∑ 50 ∑ 1 ∑ 1846 ∑ 692,4
Формулы для расчета статистических характеристик случайных величин [2]:
- выборочное среднее (среднее арифметическое) 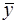 результата эксперимента определяют по формуле
результата эксперимента определяют по формуле
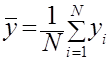 ;
; 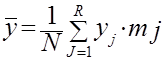 ;
;  (2.8)
(2.8)
- выборочная дисперсия S2 по формуле
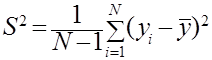 ;
; 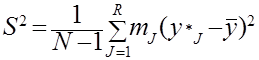 ; (2.9)
; (2.9)
- выборочное среднее квадратическое отклонение (выборочный стандарт) S по формуле
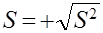 ; (2.10)
; (2.10)
- коэффициент вариации V по формуле.
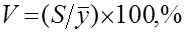 ; (2.11)
; (2.11)
- средняя ошибка среднего квадратического отклонения по формуле
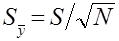 ; (2.12)
; (2.12)
- ошибка среднего квадратического отклонения по формуле
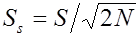 ; (2. 13)
; (2. 13)
- показатель точности среднего значения ζ * по формуле
ζ= 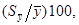 % . (2.14)
% . (2.14)
Расчетные значения статистических характеристик для рассматриваемого примера, с учетом данных вспомогательной табл. 2.4, по формулам (2.8 ….2.14) приведены в табл. 2.5.
Таблица 2.5
Значения статистических характеристик
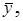 Дж/см3 Дж/см3
| S2 | S, Дж/см3 | V, % | S 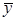 , Дж/см3 , Дж/см3
| SS, Дж/см3 | ζ , % |
| 37,0 | 14,1 | 3,75 | 0,53 | 0,38 | 1,4 |
Оценки 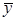 и S2 являются состоятельными и несмещенными. Оценка параметра называется состоятельной, если при неограниченном увеличении объема выборки N значения
и S2 являются состоятельными и несмещенными. Оценка параметра называется состоятельной, если при неограниченном увеличении объема выборки N значения 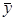 и S2 с вероятностью единица стремятся к своему теоретическому значению my и σ2y.
и S2 с вероятностью единица стремятся к своему теоретическому значению my и σ2y.
Оценка параметров называется несмещенной, если математическое ожидание my= 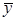 , генеральная дисперсия σ2y=S2. Несмещенность означает отсутствие систематической погрешности при оценивании параметра. Несмещенность оценки S2 достигается использованием в знаменателе формулы (2.9) величины f= N-1 вместо очевидного на первый взгляд значения N. Величину f называют числом степеней свободы. Она равна разности между числом имеющихся экспериментальных значений N, по которым вычисляют оценку дисперсии, и количеством дополнительных параметров, входящих в формулу для оценки этой дисперсии, и вычисляемых в виде линейных комбинаций тех же самых наблюдений (в данном случае это параметр
, генеральная дисперсия σ2y=S2. Несмещенность означает отсутствие систематической погрешности при оценивании параметра. Несмещенность оценки S2 достигается использованием в знаменателе формулы (2.9) величины f= N-1 вместо очевидного на первый взгляд значения N. Величину f называют числом степеней свободы. Она равна разности между числом имеющихся экспериментальных значений N, по которым вычисляют оценку дисперсии, и количеством дополнительных параметров, входящих в формулу для оценки этой дисперсии, и вычисляемых в виде линейных комбинаций тех же самых наблюдений (в данном случае это параметр 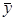 , вычисляемый по формуле (2.8)).
, вычисляемый по формуле (2.8)).
4. Определение максимальной абсолютной ошибки ∆y и доверительного интервала. При дальнейшем изложении предполагается, что результаты экспериментов подчинены нормальному закону распределения.
При ограниченных объемах испытаний необходимо указывать степень точности и надежности оценок генеральных характеристик. Представления о точности и надежности оценок дают доверительные интервалы. С вероятностью Р ошибка лежит в границах ± ∆y. Тогда истинный результат измерений my с вероятностью Р будет находиться в пределах
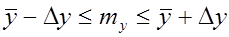 . (2.15)
. (2.15)
Вероятность Р нахождения истинного результата, равного генеральному среднему в указанных границах, называется доверительной вероятностью.
При объемах выборки n<120, для заданного уровня значимости q и числа степеней свободы f ошибка ∆y определяют из выражения
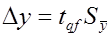 , (2.16)
, (2.16)
где tqf – табличные значения критерия t – распределения Стьюдента.
Под уровнем значимости q понимают вероятность ошибки, которой допустимо пренебречь в данном исследовании. Уровень значимости q определяют по формуле
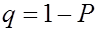 . (2.17)
. (2.17)
Определим доверительный интервал для рассматриваемого практического примера: N=50, 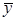 =37,0 Дж/см3,
=37,0 Дж/см3, 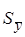 = 0,53 Дж/см3 (табл.2.5), f =50-1=49 для принятой вероятности Р=0,95 уровень значимости будет равен q=1-0,95=0,05 (форм. 2.17) или 5%. По табл. П.3 Приложения табличное значение tqf=2,01, а ошибка ∆y по формуле (2.16) равна
= 0,53 Дж/см3 (табл.2.5), f =50-1=49 для принятой вероятности Р=0,95 уровень значимости будет равен q=1-0,95=0,05 (форм. 2.17) или 5%. По табл. П.3 Приложения табличное значение tqf=2,01, а ошибка ∆y по формуле (2.16) равна
∆y=2,01  0,53=1,07 Дж/см3.
0,53=1,07 Дж/см3.
Окончательно доверительный интервал составит
37,0-1,07 ≤ my ≤ 37,0+1,07
Таким образом, с вероятностью Р=0,95 среднее значение удельной работы резания К3=y3 при фрезеровании заключено между ее значениями 35,93 и 38,07. Из 100 замеров К3 при принятых условиях фрезерования 95 ее значений будут находиться в найденном интервале.
5. Определение минимального числа повторных опытов. Необходимое количество опытов (наблюдений) n определяют из условия
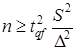 , (2.18)
, (2.18)
где ∆ - минимальная абсолютная погрешность, в примере ∆y=1,07.
Требуемое количество опытов n, необходимое и достаточное по формуле (2.18), равно для принятых выше tqf=2,01 и S2=14,1
n1=(2,012  14,1)/1,072=49.
14,1)/1,072=49.
Это количество опытов, достаточное для получения результата с абсолютной погрешностью 0,03 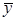 . Для получения значений удельной работы резания с погрешностью ∆=0,05
. Для получения значений удельной работы резания с погрешностью ∆=0,05 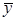 требуется поставить n2 опытов
требуется поставить n2 опытов
n2=(2,012  14,1)/(0,05
14,1)/(0,05  37,0)2=17
37,0)2=17
6. Выявление промахов. Грубые наблюдения (промахи) подлежат исключению из выборки. Чаще всего сомнения вызывают крайние элементы ранжированного ряда. Для обнаружения промахов применяют специальное τ(q,n) распределение
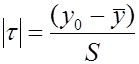 , (2,19)
, (2,19)
где - 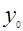 - значение проверяемого элемента выборки.
- значение проверяемого элемента выборки.
С помощью этого распределения возможно установить τ – критерий совместимости крайнего элемента выборки с остальными. При этом не используется никаких других сведений, кроме самой выборки. Согласно τ- критерию, крайнее значения y0 (ymin, ymax) отбрасывается с уровнем значимости q, если
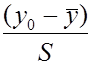 >
> 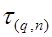 . (2.20)
. (2.20)
Значения τ(q,n) для различных объемов выборок n и уровней значимости q приведены в табл. П.4 Приложения.
В качестве примера проведем проверку крайних элементов, приведенного выше вариационного ряда: ymin=31,2; ymax=44,1; 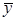 =37,0 и S=3,75 (табл.2.5). Вычислим значения максимального относительного отклонения
=37,0 и S=3,75 (табл.2.5). Вычислим значения максимального относительного отклонения 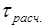 для ymin и ymax соответственно по формуле (2.19)
для ymin и ymax соответственно по формуле (2.19)
для ymin - 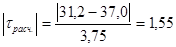 ,
,
для ymax - 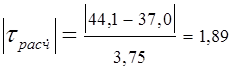 .
.
По табл. П.4 определяем табличное значение τ(q,n) для выбранного уровня значимости q и числа измерений n=50:
при q=10% τтаб = 2,80,
q=5% τтаб= 2,99,
q=1% τтаб= 3,37.
Крайние элементы отбрасываются, если τрасч> τтаб. В нашем случае ни при одном уровне значимости τрасч не превышает τтаб. Следовательно, нулевая гипотеза о возможных промахах при измерении крайних значений вариационного ряда отвергается.
Для обнаружения грубых наблюдений может быть использован t- критерий Стьюдента. Процедура обнаружения промаха включает следующие действия:
- сомнительные результаты ymin и ymax временно исключаются из выборки;
- по оставшимся наблюдениям вновь рассчитывают выборочное среднее 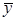 и дисперсию S2;
и дисперсию S2;
- определяют расчетное значение t-критерия Стьюдента tрасч= 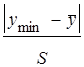 ,
,
- по табл. П.3 Приложения для принятых значений q и f определяют tтабл – табличное значение критерия Стьюдента.
Если tрасч> tтабл ,то сомнительный результат является промахом и исключается из выборки.
7. Диаграмма наклонных частот [6]. Аналитическими выражениями законов распределения случайных величин являются функции распределения вероятностей – интегральная и дифференциальная.
Интегральная функция распределения F(y) случайной величины Y показывает вероятность того, что случайная величина не превышает некоторого заданного текущего значения y
F(y)=P{Y≤y}.
Следовательно, вероятность того, что значение случайной величины Y заключено между y1 и y2, равна разности значений функции распределения в этих двух точках
P{y1<Y≤y2}=F(y2)- F(y1). (2.21)
Эмпирическим аналогом интегрального закона распределения является диаграмма накопленных частиц 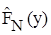 . Диаграмму строят в соответствии с формулой [6]
. Диаграмму строят в соответствии с формулой [6]
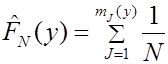 , (2.22)
, (2.22)
где mJ(y) – число элементов в выборке, для которых значение yJмин< 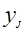 <yJmin+ΔJ, J=1,2…R. Практически это делается следующим образом. Значение наблюдений на оси ординат левее точки ymin, отложенной по оси абсцисс, равно нулю. В остальных точках ymin+∆J диаграмма имеет скачек, равный mJ/N. Для значений y=ymax=ymin+R∆ значение диаграммы накопленных частот равно 1. Если N→∞ то
<yJmin+ΔJ, J=1,2…R. Практически это делается следующим образом. Значение наблюдений на оси ординат левее точки ymin, отложенной по оси абсцисс, равно нулю. В остальных точках ymin+∆J диаграмма имеет скачек, равный mJ/N. Для значений y=ymax=ymin+R∆ значение диаграммы накопленных частот равно 1. Если N→∞ то 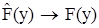 .
.
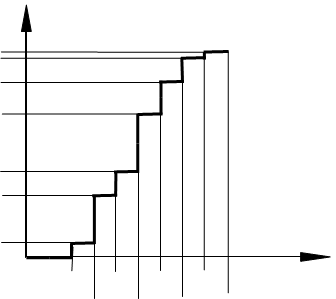
Используя данные примера (табл. 2.4, значения P*J) построим соответствующую диаграмму (рис. 2.2)
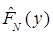
1,00
0,98
0,86
0,70
0,42
0,30
0,08 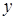
0 30,65 34,65 38,65 42,65
32,65 36,65 40,65 44,65
Рис. 2.2. Диаграмма накопленных частот
8. Гистограмма выборки [6]. Если функция F(y) дифференцируема для всех значений случайной величины Y, то закон распределения вероятности может быть выражен в аналитической форме также с помощью дифференциальной функции распределения вероятности
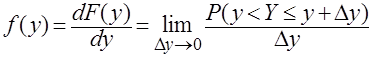 , (∆y>0). (2.23)
, (∆y>0). (2.23)
Значение функции f(y) приближенно равно отношению вероятности попадания случайной величины в интервал (y, y+∆y) к длине ∆y этого интервала, когда ∆y – бесконечно малая величина. Функцию f(y) называют также функцией плотности распределения вероятностей (функция плотности вероятности).
Гистограмма выборки fN(y) является эмпирическим аналогом функции плотности распределения f(y). Гистограмму строят следующим образом – выполняют все действия по П.2: определяют количество интервалов (форм.2.2), длину и границы интервалов (форм.2.3, 2.4), подсчитывают количество наблюдений mJ, попавших в каждый интервал (табл. 2.3), относительные частоты P*J наблюдений, попавших в данный интервал J (табл.2.4).
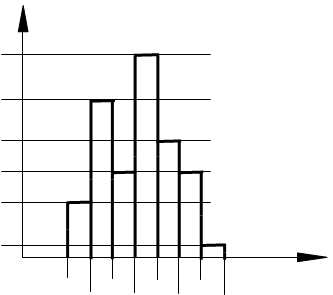
Используя данные примера для удельной работы резания, приведенные в табл. 2.4, построим соответствующую гистограмму (рис. 2.3). На оси абсцисс откладываем границы интервалов (см. рис. 2.1), а на оси ординат относительную частоту P*J. На основании, равном длине интервала, строим примыкающие друг к другу прямоугольники, высота которых равна относительной частоте P*J наблюдений, попавших в J-ый интервал (рис. 2.3).
 fN(y)
fN(y)
0,28
0,22
0,16
0,12
0,08
0,02 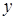
0 30,65 34,65 38,65 42,65
32,65 36,65 40,65 44,65
Рис. 2.3. Гистограмма выборки
Лабораторная работа № 3
ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
Дата добавления: 2014-12-05; просмотров: 1140;
