Указания к выполнению работы
Планирование эксперимента – это процедура выбора числа и условий проведения опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью. Число возможных различных опытов обычно велико, поэтому возникает вопрос их ограничения. Это с неизбежностью приводит к необходимости планирования эксперимента. Методика (техника) планирования эксперимента зависит от типа планов с соответствующими процедурами планирования.
Рассмотрим процедуру планирования эксперимента для отдельных типов планов на практическом примере конкретной научно-технической задачи.
1. Словесная формулировка научно-технической задачи включает сведения о совокупности идентификаторов исследуемого процесса (объекта), ожидаемом результате и условиях протекания процесса (совокупностях признаков), известных, необходимых для получения этого результата и неизвестных.
Словесная формулировка задачи приведена в  выданном варианте задачи и требует только уточнения в части идентификаторов и условий исследуемого процесса на основе знаний, полученных при изучении дисциплин специальности.
выданном варианте задачи и требует только уточнения в части идентификаторов и условий исследуемого процесса на основе знаний, полученных при изучении дисциплин специальности.
Пример словесной формулировки задачи: исследовать касательные силы резания FX при токарной обработке деталей в зависимости от подачи на резец SO и угла резания d в дереворежущих токарных станках.
2. Математическая формулировка задачи включает перечень:
а) переменных факторов и диапазон их варьирования:
- подача на резец SO º x 1 и угол резания d º x 2;
- диапазоны варьирования переменных факторов (условий процесса)
принимаем для подачи на резец 0,2 мм/об £ SO £ 0,8 мм/об, а для угла резания 25° £ d £ 45°;
б) постоянных факторов и их уровней:
- порода – береза, влажность – 22%, частота вращения детали h=120 мин –1, радиус затупления лезвия r=4 мкм, точение осевое;
в) оценочных показателей – касательная сила резания, диапазон ее изменения Fx = 5…40 Н.
3. Определение уровней и интервалов варьирования факторов.
Верхние нижние и уровни факторов, соответственно минимальные и максимальные значения для их натуральных значений в исследовании установлены выше в П. 2.2. а: 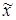 1 min = 0,2 мм/об;
1 min = 0,2 мм/об; 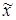 1 max = 0,8 мм/об;
1 max = 0,8 мм/об; 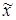 2 min = 25° и
2 min = 25° и 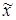 2 max = 45°.
2 max = 45°.
Основной уровень фактора 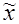 i 0 определяют по формуле:
i 0 определяют по формуле:
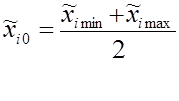 .(1.1)
.(1.1)
Значения основного уровня для подачи на резец по формуле (1.1) 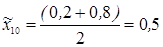 мм/об, угла резания
мм/об, угла резания 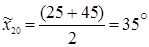 .
.
Интервал варьирования определяют по формуле:
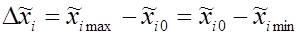 . (1.2)
. (1.2)
Значения интервалов варьирования 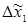 и
и 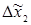 для факторов
для факторов 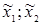 по формуле (1.2) будут составлять:
по формуле (1.2) будут составлять: 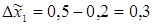 мм/об,
мм/об, 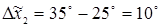 .
.
Переход от натуральных значений факторов к нормализованным (кодированным) значениям 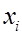 выполняют по формуле
выполняют по формуле
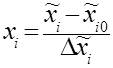 . (1.3)
. (1.3)
Вычисляют по формуле (1.3) уровни и интервалы варьирования для нормализованных значений и факторов в исследовании
для подачи на резец
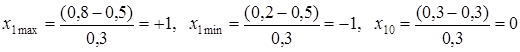 ;
;
для угла резания
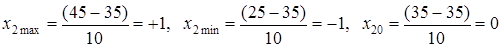 .
.
4. Матрица планирования полного факторного эксперимента типа ПФЭ 2K (к - количество факторов, r=2 – количество уровней, на которых варьируется каждый фактор).
Планом полного факторного эксперимента называют такие планы экспериментов, в которых факторы варьируются на двух уровнях, а все возможные комбинации этих уровней встречаются одинаковое количество раз. В планировании эксперимента используются нормализованные значения факторов +1 и –1. Условия эксперимента можно записать в виде таблицы, где строки соответствуют различным опытам (вектор-строка), а столбцы – значениям факторов (вектор-столбец). Такие таблицы называются матрицами планирования экспериментов (МПЭ).
Для случая K переменных факторов и при их варьировании только на двух нижнем и верхнем уровнях (r=2) число опытов N для всех возможных сочетаний уровней факторов определяют по формуле
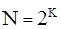 . (1.4)
. (1.4)
На основании изложенного, матрица плана полного факторного эксперимента в общем виде может быть представлена в виде табл.1.1.
Таблица 1.1
Матрица плана ПФЭ 2 К (К=2) в общем виде
| Номер опыта | Значения факторов | Значение
выходной
величины
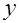
| |
 1 1
|  2 2
| ||
 1 min 1 min
 1 max 1 max
 1 min 1 min
 1 max 1 max
|  2 min 2 min
 2 min 2 min
 2 max 2 max
 2 max 2 max
| 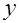 1 1
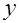 2 2
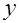 3 3
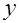 4 4
|
Для проведения эксперимента пользуются матрицей в явном виде или рабочей матрицей, приведенной в табл. 1.2.
Таблица 1.2
Рабочая матрица ПФЭ 2 К (К=2)
| Номер опыта | Натуральные значения факторов | Нормализованные значения факторов | Значение выходной величины
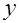
| ||
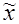 1, мм/об 1, мм/об
| 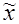 2, град 2, град
|  1 1
|  2 2
| ||
| 0,2 0,8 0,2 0,8 | - 1 +1 - 1 +1 | - 1 - 1 +1 +1 | 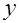 1 1
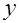 2 2
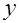 3 3
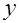 4 4
|
Для удобства расчета коэффициентов уравнения регрессии составляется расчетная матрица (или расширенная расчетная матрица) полного факторного эксперимента, представленная в табл. 1.3.
Таблица 1.3
Расчетная матрица ПФЭ 2 К (К=2)
| Номер опыта |  0 0
|  1 1
|  2 2
|  3= 3=  1 1  2 2
| Значение выходной величины
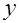
|
| +1 +1 +1 +1 | - 1 +1 - 1 +1 | - 1 - 1 +1 +1 | +1 - 1 - 1 +1 | 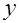 1 1
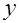 2 2
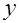 3 3
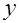 4 4
|
Вектор-столбец  0 вводится для расчета коэффициента при нулевой степени значения фактора, а вектор-столбец
0 вводится для расчета коэффициента при нулевой степени значения фактора, а вектор-столбец  3 – для расчета коэффициента во взаимодействиях факторов
3 – для расчета коэффициента во взаимодействиях факторов  1
1  2.
2.
Уравнение, в виде которого представляется математическая модель, называется уравнением регрессии. Уравнение регрессии чаще всего записывают отрезком степенного ряда – алгебраическим полиномом. По результатам ПФЭ можно построить математическую модель, содержащую линейные члены и взаимодействие первого порядка
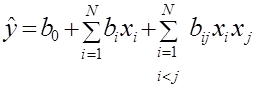 ,(1.5)
,(1.5)
где 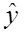 - расчетное значение выходной величины;
- расчетное значение выходной величины;
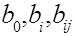 - коэффициенты, определяемые по результатам эксперимента,
- коэффициенты, определяемые по результатам эксперимента,
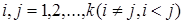 .
.
Для нашего примера выражение (1.5) примет вид
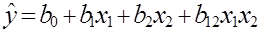 . (1.6)
. (1.6)
Общий анализ математической модели (1.6) включает анализ оценки знака при коэффициентах b0, b1, b2, b12 на значение выходной величины 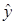 , относительной значимости факторов по абсолютной величине коэффициентов, важности установленной зависимости.
, относительной значимости факторов по абсолютной величине коэффициентов, важности установленной зависимости.
5. Матрица планирования для B-плана (плана Бокса). B-планы используются для построения планов 2-го порядка. Планами 2-го порядка называются такие планы многофакторного эксперимента, с помощью которых можно получить математическое описание объектов в виде полинома 2-го порядка. В общем случае для К факторов уравнение регрессии, записанное в виде полинома 2-го порядка, будет иметь вид
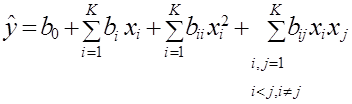 . (1.7)
. (1.7)
Число коэффициентов регрессии r такого плана определяют по формуле
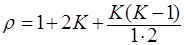 . (1.8)
. (1.8)
Уравнение (1.7) позволяет оценить коэффициенты регрессии 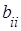 при
при
квадратичных членах 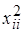 , дает более детальное описание объекта, в связи с чем планы 2-го порядка часто используются на заключительном этапе эксперимента. В этих планах каждый фактор варьируется не менее чем на трех уровнях.
, дает более детальное описание объекта, в связи с чем планы 2-го порядка часто используются на заключительном этапе эксперимента. В этих планах каждый фактор варьируется не менее чем на трех уровнях.
Составной частью В-плана является план ПФЭ 2К. Поставив дополнительно некоторое число опытов, получают В-план в целом и соответствующую математическую модель в виде полинома 2-го порядка. Это свойство В-плана называют композиционностью. Факторы в В-планах варьируются на трех уровнях: -1; 0; +1 в нормализованных обозначениях.
Назовем звездной точкой В-плана условия опыта, в котором один из факторов принимает значение +1 или –1, а остальные значения факторов фиксируются на основном уровне (ноль в нормализованных значениях). Например, звездная точка для трех факторов: x1= +1, x2=0, x3=0 и т.д. Очевидно, для K факторов имеется 2 K различных точек, а общее число опытов N В-плана составит
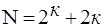 . (1.9)
. (1.9)
Матрица планирования В-плана для двух факторов приведена в табл. 1.4 (число опытов по формуле (1.9) будет равно N=22+2 2=8).
Таблица 1.4
Матрица планирования В-плана, K=2
| Наименование составной части В-плана | Номер опыта | Значение фактора | Значение
выходной величины
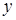
| |
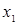
| 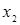
| |||
| Ортогональная часть В-плана (ПФЭ 2К) | -1 +1 -1 +1 | -1 -1 +1 +1 | y1 y2 y3 y4 | |
| Звездная часть | -1 | y5 |
Окончание табл.1.4
| В-плана | +1 | -1 +1 | y6 y7 y8 |
6. Матрица планирования для униформ-рототабельного плана (УРП) второго порядка. Каждый фактор УРП 2-го порядка, варьируются на пяти уровнях: -a, -1, 0, +1.+a, где a носит название звездного плеча – число больше единицы.
Число a используют при построении некоторых опытов, которые входят в УРП и называются звездными точками плана. В этих опытах один фактор фиксируют на уровнях ±a, а остальные - на основном. Таких опытов в УРП – 2К. Звездное плечо a определяется из выражения для ПФЭ 2К:
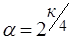 , (1.10)
, (1.10)
дробного факторного эксперимента (ДФП):
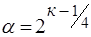 . (1.11)
. (1.11)
В УРП входят опыты ПФЭ 2К, звездные точки – 2К и некоторое количество точек в центре плана. Число центральных точек nц выбирается из условия униформности плана и может быть принято: nц=5для К=2, nц=6 для К=3 и nц=7 для К=4.
С учетом изложенного, матрица планирования униформ-рототабельного плана для двух факторов в нормализованных обозначениях может быть представлена в форме табл. 1.5 (число опытов N=22+2 2+5=13 по формуле (1.10) 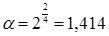 ).
).
Таблица 1.5
Матрица планирования УРП для К=2
| Наименование составной части УРП | Номер опыта | Значение фактора | Значение
выходной величины
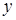
| |
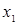
| 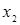
| |||
| Ортогональная часть УРП (ПФЭ 2К) | -1 +1 -1 +1 | -1 -1 +1 +1 | y1 y2 y3 y4 | |
| Звездная часть УРП | -1,414 +1,414 | -1,414 +1,414 | y5 y6 y7 y8 |
Окончание табл.1.5
| Опыты в центре УРП | y9 y10 y11 y12 y13 |
Уравнение регрессии в виде полинома 2-го порядка для двух факторов 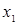 и
и 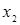 для нашего случая, с учетом выражения (1.7), будет иметь вид
для нашего случая, с учетом выражения (1.7), будет иметь вид
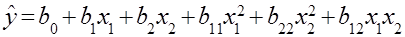 . (1,12)
. (1,12)
Дата добавления: 2014-12-05; просмотров: 1467;
