От температуры. Закон Кирхгофа
Отношение бесконечно малого количества теплоты, сообщаемой телу, к тому изменению температуры, которое этим вызывается, называется истинной теплоемкостью:
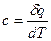
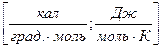 (12)
(12)
Для изохорных процессов
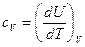 . (13)
. (13)
Для изобарных процессов
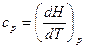 . (14)
. (14)
Эти равенства справедливы для любых веществ и для любого агрегатного состояния.
Для изохорного процесса тепловой эффект определяется величиной изменения внутренней энергии системы DU=U2-U1. Дифференцируя это равенство по температуре, получаем
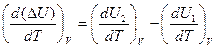 .
.
Так как 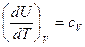 , то
, то
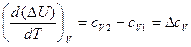 , (15)
, (15)
где сV1 и сV2 – изохорные теплоемкости системы в начальном и конечном состояниях, ΔсV – изменение изохорной теплоемкости при переходе из состояния 1 в состояние 2.
Аналогично для изобарного процесса:
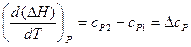 . (16)
. (16)
В общем случае
 (17)
(17)
Уравнения (15) и (16) выражают закон Кирхгофа:
температурный коэффициент теплового процесса равен изменению теплоемкости системы, происходящему в результате процесса.
Тепловой эффект реакции при любой температуре и давлении, не сильно превышающем одну атмосферу, может быть рассчитан по уравнению Кирхгофа:
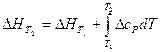 , (18)
, (18)
где ΔсР – разность между суммой изобарных теплоемкостей веществ, стоящих в правой части уравнения реакции, взятых с учетом стехиометрических коэффициентов, и такой же суммой теплоемкостей веществ, стоящих в левой части уравнения; 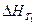 - тепловой эффект реакции при температуре Т1.
- тепловой эффект реакции при температуре Т1.
Расчет может быть выполнен, если известны величина теплового эффекта реакции при какой-либо температуре Т1 (например, стандартной) и температурная зависимость теплоемкостей веществ, участвующих в реакции, в интервале Т1-Т2.
Таким образом, чем больше разность между теплоемкостями продуктов реакции и исходных веществ, тем сильнее зависимость теплового эффекта реакции от температуры.
Если теплоемкость с ростом температуры остается неизменной DсP=0 и 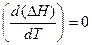 , то изменение температуры не влияет на тепловой эффект реакции.
, то изменение температуры не влияет на тепловой эффект реакции.
Зависимость теплоемкости от температуры обычно выражается эмпирическими приближенными уравнениями вида:
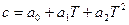
или 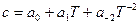 .
.
Если зависимость с(Т) известна в такой форме для всех веществ, участвующих в реакции, то по уравнению (17) определяют Δс=f(Т). Полученное выражение ( 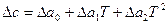 или
или 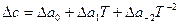 ) подставляют в уравнение Кирхгофа (18) и интегрируют его.
) подставляют в уравнение Кирхгофа (18) и интегрируют его.
Пример. Составим уравнение температурной зависимости теплового эффекта реакции восстановления железа кремнием:
2FeO + Si = SiO2 + 2Fe.
Исходные данные для расчета приведены в таблице.
Таблица
| Реагенты реакции | 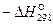 , , 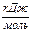
| 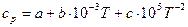
| ||
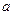
| 
| 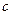
| ||
| FeO | 269,42 | 51,87 | 6,79 | -1,59 |
| Si | - | 24,13 | 2,35 | -4,57 |
| SiO2 | 880,74 | 47,01 | 34,36 | -11,31 |
| Fe | - | 17,51 | 24.80 | - |
Определим температурную зависимость приращения теплоемкости процесса по уравнению:
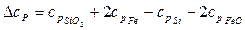 .
.
Можно вместо теплоемкостей веществ реакции подставить соответствующие выражения их температурной зависимости и привести выражение к стандартному виду или рассчитать коэффициенты уравнения и подставить их в уравнение
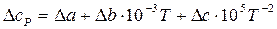 .
.
Рассчитаем коэффициенты:
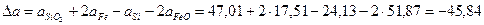
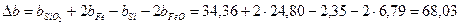
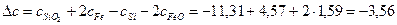
Получаем уравнение температурной зависимости приращения теплоемкости процесса:
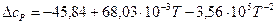 .
.
Подставив полученное выражение в уравнение Кирхгофа и проинтегрировав его в интервале температур от 0К до Т, получим уравнение зависимости теплового эффекта реакции от температуры:
 .
.
Для того чтобы найти тепловой эффект 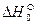 реакции при 0К, подставим
реакции при 0К, подставим 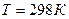 и вместо
и вместо 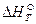 величину
величину 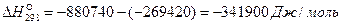 :
:
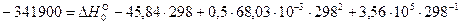
Выполнив вычисления, получаем 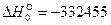 Дж/моль.
Дж/моль.
Уравнение температурной зависимости теплового эффекта реакции имеет вид: 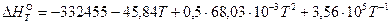 .
.
По данному уравнению можно рассчитать тепловые эффекты реакции для требуемых температур.
НАПРАВЛЕНИЕ ХИМИЧЕСКИХ РЕАКЦИЙ
Дата добавления: 2014-12-05; просмотров: 2337;
