Примеры задач линейного программирования
Задача 1. Использование сырья. Предприятие может выпускать два вида продукции 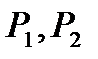 . На их изготовление расходуется три вида сырья
. На их изготовление расходуется три вида сырья 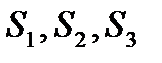 . Запасы сырья, нормы их расхода на единицу изделия, себестоимость С и оптовые цены приведены в таблице:
. Запасы сырья, нормы их расхода на единицу изделия, себестоимость С и оптовые цены приведены в таблице:
| Тип сырья | Запасы сырья | Нормы расхода сырья на изделие | |
| Р1 | Р2 | ||
| S1 | |||
| S2 | |||
| S3 | |||
| Себестоимость, усл. ед. | |||
| Цены, усл. ед. |
Требуется составить план выпуска продукции, обеспечивающий получение максимальной прибыли.
Построим математическую модель: обозначим X1 и X2 - количество выпускаемой продукции Р1 и Р2. На изготовление изделий P1, Р2 будет израсходовано 10X1 + 20X2 единиц сырья S1. По условию имеем: 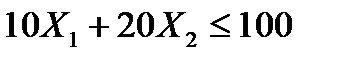 .
.
Аналогичным образом получаем ограничения по другим видам сырья: 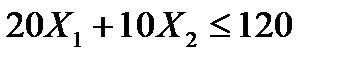 ,
, 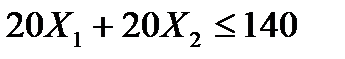
В результате реализации единицы изделия Р1 предприятие получит прибыль (7-5)=2 усл. ед.; единицы изделия Р2 - прибыль (13-10) = 3 усл. ед. Общая прибыль составит: 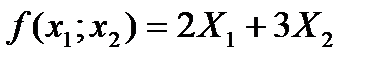 .
.
Итак, задача свелась к нахождению неотрицательных чисел X1 и X2, удовлетворяющих линейным ограничениям и обращающих в максимум линейную целевую функцию 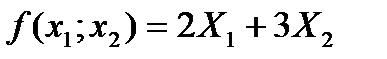 .
.
Задача 2. Задача о диете. Пусть имеется два вида продуктов 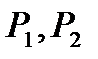 , в которые входят три вида питательных веществ, например белки, жиры и углеводы
, в которые входят три вида питательных веществ, например белки, жиры и углеводы 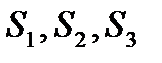 . Содержание количества единиц питательных веществ в 1 кг каждого вида продукта, норма содержания питательных веществ в дневном рационе и стоимость 1 кг продукта представлены в таблице:
. Содержание количества единиц питательных веществ в 1 кг каждого вида продукта, норма содержания питательных веществ в дневном рационе и стоимость 1 кг продукта представлены в таблице:
| Питательные вещества | Норма содержания питательных веществ | Содержание питательных веществ в 1 кг продукта | |
| P1 | P2 | ||
| S1 | |||
| S2 | |||
| S3 | |||
| Стоимость, усл. ед. |
Требуется составить такой рацион питания, при котором затраты на приобретение продуктов будут минимальными. Построим математическую модель: обозначим X1 и X2 - суточное потребление продуктов Р1 и Р2,тогда стоимость рациона определяется из следующих условий: 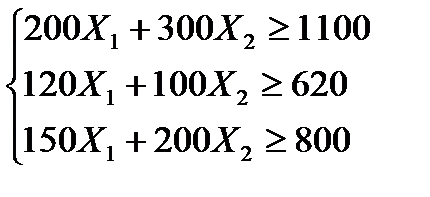
Задача свелась к нахождению неотрицательных чисел X1, X2, удовлетворяющих линейным ограничениям и доставляющих минимум линейной целевой функции 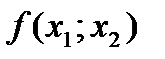 .
.
Задача 3. Транспортная задача. В двух пунктах отправления сосредоточен однородный груз в количестве 5т и 15 т. Груз необходимо доставить трем потребителям, потребности которых одинаковы: 1-й потребитель - 6 т, 2-й потребитель - 10 т, 3- й потребитель - 4 т. Известны также затраты на перевозку единицы груза из i-гo пункта отправления в каждый j-й пункт потребления:
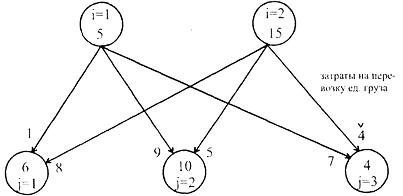
Требуется составить такой план перевозок груза, при котором общая стоимость перевозок была бы минимальной. Математическая модель: обозначим Xij - объем перевозок груза из i-гo пункта отправления в j-й пункт потребления (i = 1,2; j = 1,2,3). Тогда получим:
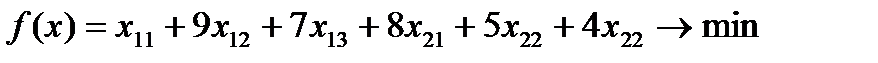 при ограничениях
при ограничениях
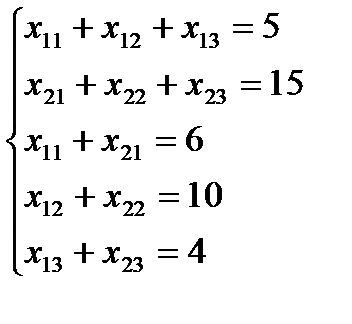
Теорема 1.2. Если задача линейного программирования имеет оптимальный план, то экстремальное значение целевая функция задачи принимает в одной из вершин многогранника решений. Если экстремальное значение целевая функция принимает более чем в одной вершине, то она принимает его на ребре (грани), содержащем эти вершины.
Дата добавления: 2014-12-05; просмотров: 1819;
