Типы оптимальных решений задач линейного программирования при решении графическим методом
При решении задач линейного программирования графическим методом возможны следующие случаи.
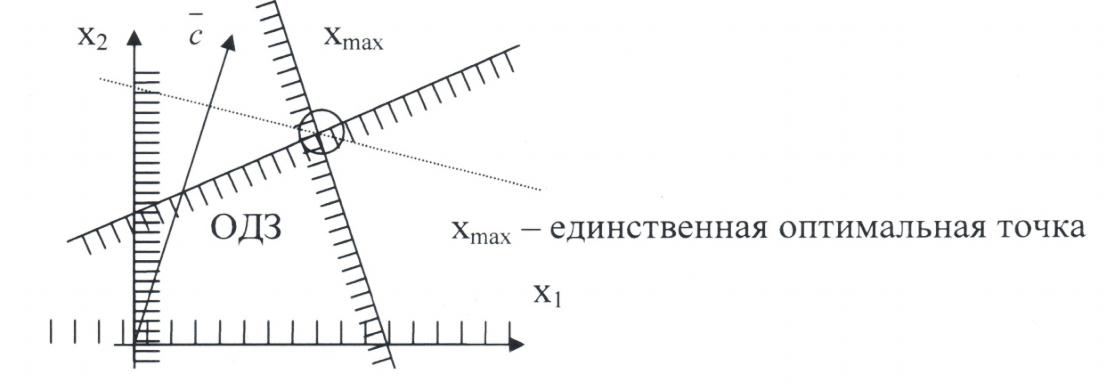 1. Единственность оптимального решения. В этом случае опорная изоцель имеет с ОДЗ только одну общую точку.
1. Единственность оптимального решения. В этом случае опорная изоцель имеет с ОДЗ только одну общую точку.
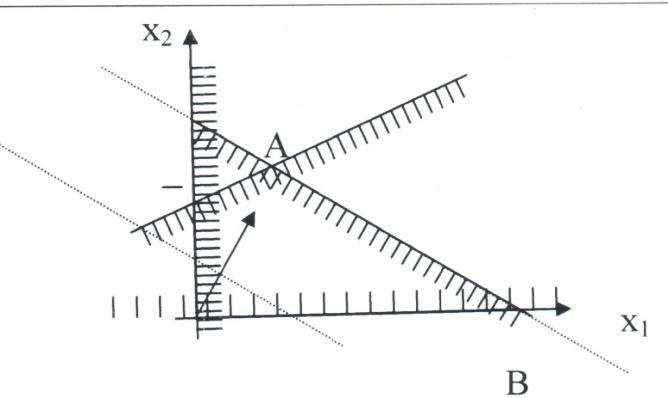 2. Альтернативный оптимум (множество оптимальных решений). В этом случае опорная изоцель совпадает с одной из сторон ОДЗ многоугольника.
2. Альтернативный оптимум (множество оптимальных решений). В этом случае опорная изоцель совпадает с одной из сторон ОДЗ многоугольника.
В данном случае целевая функция достигает своего максимального значения в любой точке отрезка [A;B]
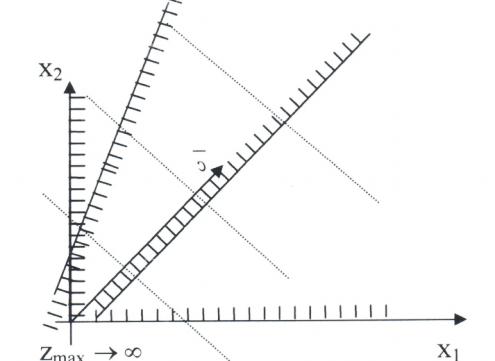
3. Задача линейного программирования не имеет оптимального решения, так как целевая функция не ограничена сверху, если требуется найти максимум целевой функции (или снизу, если требуется найти минимум).
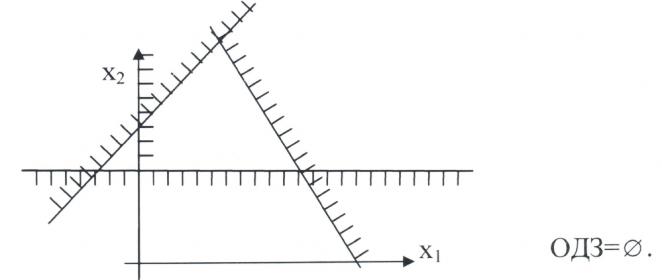 4. Задача линейного программирования не имеет решения, так как система ограничений противоречива, то есть ОДЗ=∅ .
4. Задача линейного программирования не имеет решения, так как система ограничений противоречива, то есть ОДЗ=∅ .
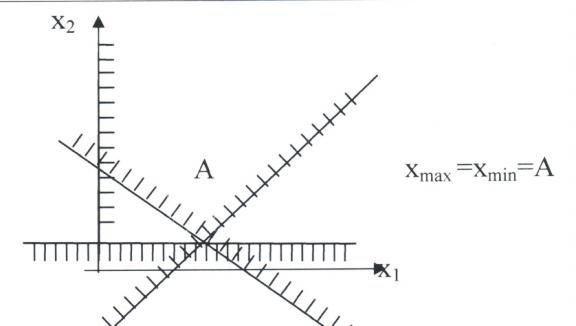 5. Если ОДЗ состоит из одной точки, то в этой точке z принимает своё максимальное и минимальное значение.
5. Если ОДЗ состоит из одной точки, то в этой точке z принимает своё максимальное и минимальное значение.
Содержание работы
Задача1 . Построить множество решений системы линейных неравенств:
1.1) 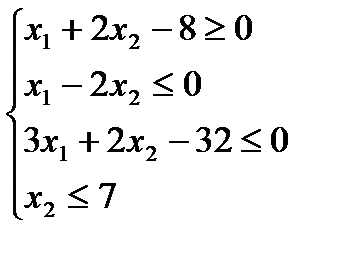 1.2)
1.2) 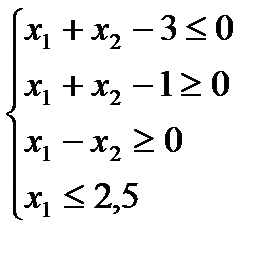 1.3)
1.3) 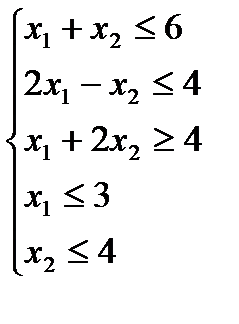
1.4) 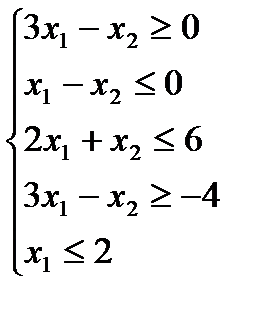 1.5)
1.5) 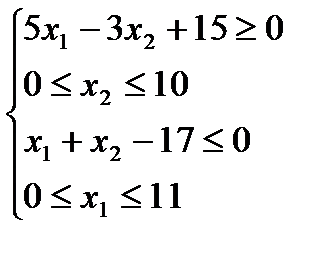
Задача2 . Решите следующие задачи линейного программирования графическим методом:
2.1) 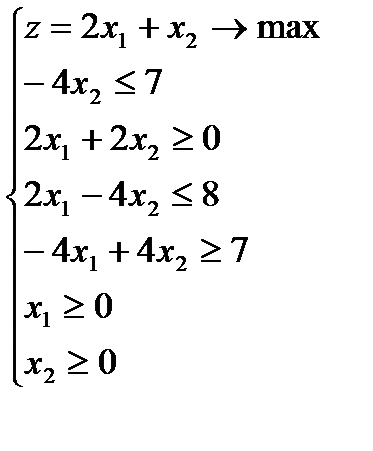 2.2)
2.2) 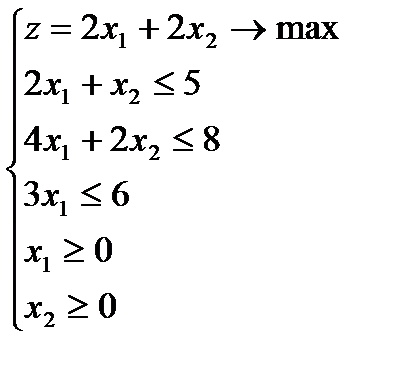 2.3)
2.3) 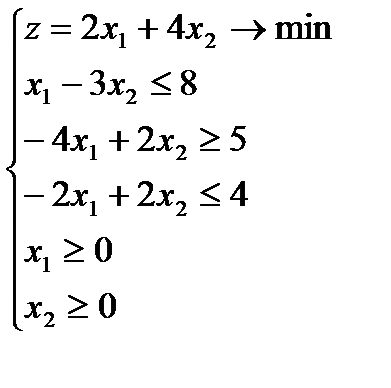
2.4) 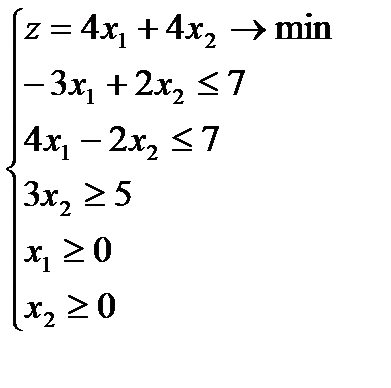 2.5)
2.5) 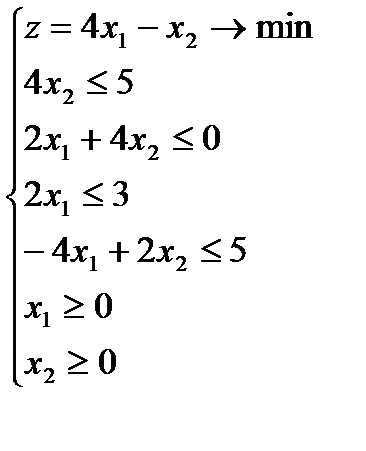
Задача3 . Решите задачи:
3.1. Для производства двух видов изделий А и В используются три типа технологического оборудования. Для производства единицы изделия А оборудование первого типа используется в течении 1 часа, оборудование второго типа – 3 часа, оборудование третьего типа – 3 часа. Для производства единицы изделия В оборудование первого типа используется в течении 2 часов, оборудование второго типа – 3 часа, оборудование третьего типа – 1 час. На изготовление всех изделий предприятие может использовать оборудование первого типа не более чем 32 часа, оборудование второго типа – 60 часов, оборудование третьего типа – 50 часов. Прибыль от реализации единицы готового изделия А составляет 4 денежные единицы, а изделия В – 2 денежные единицы.
Составить план производства изделий А и В, обеспечивающий максимальную прибыль от их реализации.
| Виды технологического оборудования | Время на производство изделий | Предел часов на производство | |
| А | В | ||
| Прибыль от реализации изделий | 4 усл.ед. | 2 усл.ед. |
3.2. При составлении суточного рациона кормления скота можно использовать свежее сено не более 50 кг и силос не более 85 кг. Рацион должен содержать не менее 30 кормовых единиц, 1000 г белка, 100 г кальция и 80 г фосфора. Определить оптимальный рацион, исходя из условия минимума себестоимости. В таблице приведены данные о содержании указанных компонентов в 1 кг каждого корма и себестоимость этих кормов.
Таблица – Исходные данные задачи о рационе
| Корм | Компоненты | Себестоимость, ден. ед. | |||
| кормовые единицы | белок, г/кг | кальций, г/кг | фосфор, г/кг | ||
| Сено свежее, кг | 0,5 | 1,25 | 1,2 | ||
| Силос, кг | 0,5 | 2,5 | 0,8 |
3.3. Фирма выпускает изделия двух видов А и В. Изделия каждого вида обрабатывают на двух станках (I и II). Время обработки одного изделия каждого вида на станках, время работы станков за рабочую смену, прибыль фирмы от реализации одного изделия вида А и вида В занесены в таблицу:
| Станки | Время обработки одного изделия, мин. | Время работы станка за смену, мин. | |
| А | В | ||
| I | |||
| II | |||
| Прибыль от одного изделия, усл.ед. | 0,3 | 0,9 |
Изучение рынка сбыта показало, что ежедневный спрос на изделия вида В никогда не превышает спрос на изделия вида А более чем на 40 единиц, а спрос на изделия вида А не превышает 90 единиц в день.
Определить план производства изделий, обеспечивающий наибольшую прибыль.
3.4. Предприятие электронной промышленности выпускает две модели радиоприемников, причем каждая модель производится на отдельной технологической линии. Суточный объем первой линии - 60 изделий, второй линии - 80 изделий. На радиоприемник первой модели расходуется 15 однотипных элементов электронных схем, на радиоприемник второй модели - 10 таких же элементов. Максимальный суточный запас используемых элементов равен 950 единиц. Прибыли от реализации одного радиоприемника первой и второй моделей равны 40 усл.ед. и 20 усл.ед соответственно. Определите оптимальные суточные объемы производства первой и второй моделей.
3.5. Менеджер предприятия, изготавливающего два вида красок, описал исследователю операций ситуацию, сложившуюся на производстве и рынке сбыта красок. Оказалось, что фабрика изготавливает два вида красок: для внутренних и внешних работ. Обе краски поступают в оптовую продажу. Для производства красок используются два исходных продукта – А и В. Максимально возможные суточные запасы этих продуктов 6 и 8 тонн соответственно. Опыт показал, что суточный спрос на внешнюю краску никогда не превышает спрос на внутреннюю более чем на 1 тонну. Кроме того, установлено, что спрос на внешнюю краску никогда не превышает 2 тонны в сутки. Оптовые цены одной тонны красок сложились следующим образом: 3 тысячи рублей на внешнюю краску и 2 тысячи рублей – на внутреннюю. Какое количество краски каждого вида должна производить фабрика, чтобы доход от реализации был максимальным?
Дата добавления: 2014-12-05; просмотров: 4658;
