Алгоритм графического метода
1. Проверяется находится ли исходная ЗЛП в стандартной форме, если нет, то задачу необходимо преобразовать к стандартной форме.
2. Определяется количество неизвестных переменных. Если это количество больше трёх, то задача не может быть решена графическим методом. Существуют другие эффективные методы решения таких задач.
3. Строится область допустимых значений переменных для ЗЛП.
4. Строится направляющий вектор c .
5. Перпендикулярно направляющему вектору через ОДЗ проводится исходная изоцель.
6. Проводится мысленное перемещение исходной изоцели в направлении вектора c , если определяется максимальное значение целевой функции или в противоположном направлении, если определяется её минимальное значение, до тех пор, пока изоцель не станет опорной к ОДЗ. Точки пересечения опорной изоцели и ОДЗ и будут оптимальными точками задачи.
7. Для определения координат оптимальной точки, необходимо решить систему соответствующих линейных уравнений.
8. Для нахождения оптимального значения целевой функции, необходимо оптимальные значения переменных подставить в целевую функцию и вычислить её значение.
Пример1. Решить следующую задачу линейного программирования графическим методом:
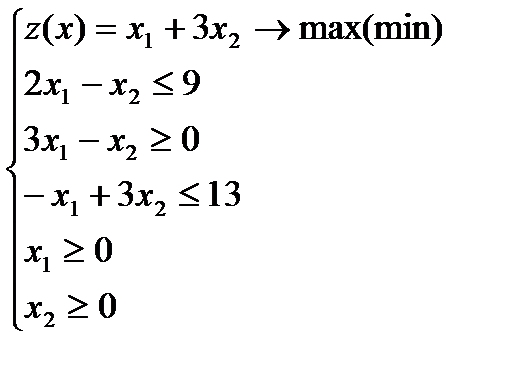
Решение.
Задача находится в стандартной форме и имеет две переменные и, следовательно, может быть решена графическим методом.
Строим ОДЗ для переменных задачи.
1) 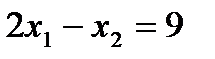
| x1=0 | x2=-9 |
| x1=9/2 | x2=0 |
По этим двум точкам строим прямую. Определяем, какая из полуплоскостей является решением данного неравенства. Для этого подставляем координаты любой точки, не принадлежащей прямой, в первое неравенство. Для простоты вычислений возьмём точку (0;0). Получим: 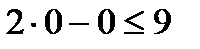 . Такое неравенство является истинным и, следовательно, полуплоскость, на которой расположена точка (0;0), является искомой.
. Такое неравенство является истинным и, следовательно, полуплоскость, на которой расположена точка (0;0), является искомой.
2) 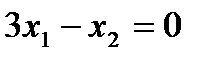 . Данная прямая проходит через начало координат, поэтому необходимо взять одну точку (0;0), а вторую – любую другую, удовлетворяющую данному уравнению. Например, точку (1;3)
. Данная прямая проходит через начало координат, поэтому необходимо взять одну точку (0;0), а вторую – любую другую, удовлетворяющую данному уравнению. Например, точку (1;3)
| x1=0 | x2=0 |
| x1=1 | x2=3 |
3) 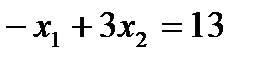
| x1=0 | x2=13/3 |
| x1=-13 | x2=0 |
4) 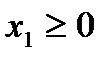 – это правая полуплоскость системы координат.
– это правая полуплоскость системы координат.
5) 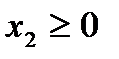 – это верхняя полуплоскость системы координат.
– это верхняя полуплоскость системы координат.
Найдём пересечение всех построенных полуплоскостей. Это будет многоугольник ABDE.
Построим направляющий вектор c = (1;3) и исходную изоцель. Сначала решаем задачу на нахождение максимального значения целевой функции. Для этого мысленно перемещаем изоцель в направлении градиента целевой функции. Она станет опорной в точке D. Решая систему из двух соответствующих уравнений, находим оптимальные значения переменных: 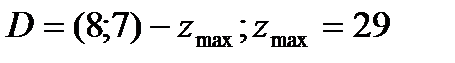
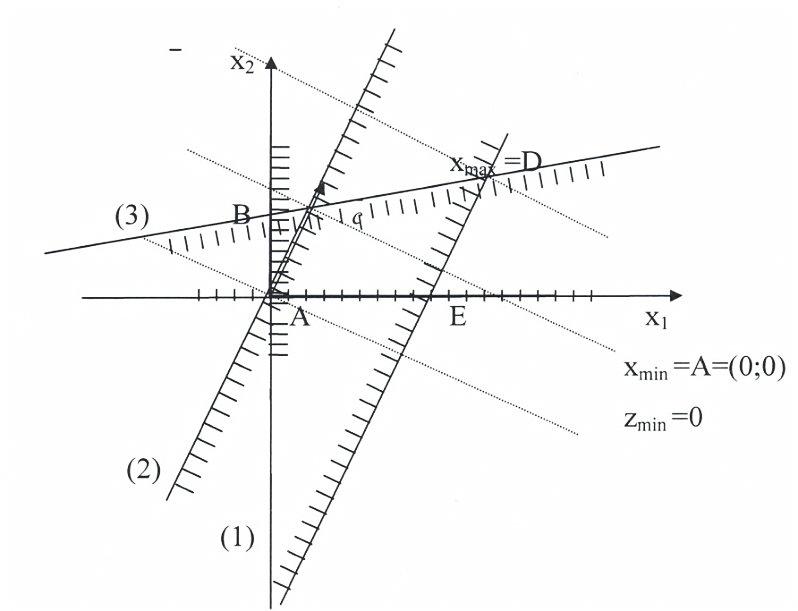 Для решения задачи на нахождение минимального значения целевой функции перемещаем исходную изоцель в направлении противоположном градиенту целевой функции. Изоцель станет опорной в точке (0;0). Ответ:
Для решения задачи на нахождение минимального значения целевой функции перемещаем исходную изоцель в направлении противоположном градиенту целевой функции. Изоцель станет опорной в точке (0;0). Ответ: 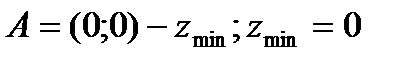
Пример2. Для изготовления двух видов продукции используется три вида сырья. При производстве единицы продукции первого вида затрачивается 13 кг сырья первого вида, 4 кг сырья второго вида и 3 кг третьего вида. При производстве единицы продукции второго вида затрачивается 2 кг сырья первого вида, 4 кг сырья второго вида и 14 кг третьего вида. Запасы сырья первого вида составляют 260 кг, второго – 124 кг, третьего – 280 кг. Прибыль от реализации единицы продукции первого вида составляет 12усл.ед., а прибыль от реализации единицы продукции второго вида составляет 10 усл.ед.. Построить экономико-математическую модель задачи, максимизирующую прибыль от реализации продукции. Решить задачу геометрическим методом.
Запишем данные задачи в виде таблицы
| Вид сырья | Расход сырья на единицу продукции | Запас сырья | |
| I | II | ||
| Прибыль от реализации единицы продукции |
Построим экономико-математическую модель задачи.
Целевая функция 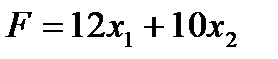
Система ограничений 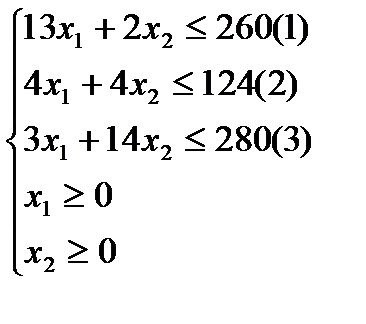
Задание: максимизировать целевую функцию . 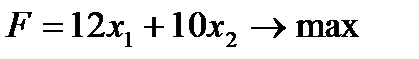
Геометрический метод решения.
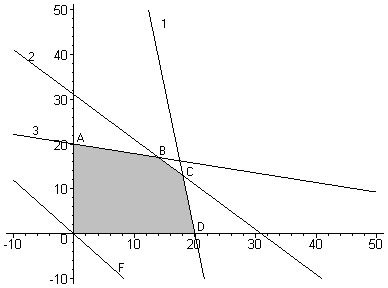
Найдем множество точек плоскости, координаты которых удовлетворяют системе ограничений. Многоугольник OABCD – область допустимых решений. Среди точек многоугольника выберем такую, в которой целевая функция достигает максимального значения. Для этого по уравнению 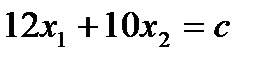 строим несколько линий уровня
строим несколько линий уровня 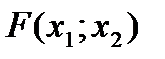 , произвольно выбирая с. Последней вершиной, к которой прикоснется прямая
, произвольно выбирая с. Последней вершиной, к которой прикоснется прямая 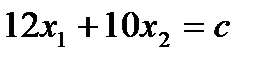 при выходе за границу многоугольника допустимых решений системы ограничений, будет точка С. В точке С пересекаются две прямые, поэтому для нахождения координат точки достаточно решить систему уравнений:
при выходе за границу многоугольника допустимых решений системы ограничений, будет точка С. В точке С пересекаются две прямые, поэтому для нахождения координат точки достаточно решить систему уравнений:
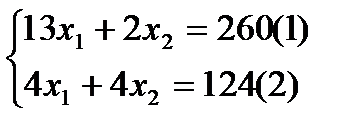
В результате получаем: (18;13). Полученное решение будет оптимальным производственным планом, дающим максимальную прибыль.
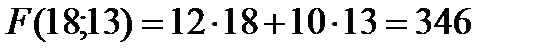 руб.
руб.
Ответ: чтобы максимизировать прибыль от реализации продукции необходимо выпускать 18 единиц продукции первого вида и 13 единиц продукции второго вида.
Дата добавления: 2014-12-05; просмотров: 3713;
