Решение систем линейных неравенств с двумя переменными.
Пример1. Решить графически систему:
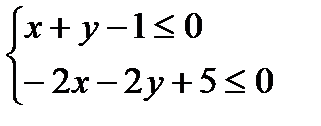
Решение:
1) Рассмотрим уравнения  и
и 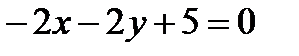 , соответствующие неравенствам;
, соответствующие неравенствам;
2) 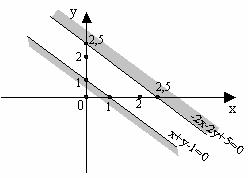 Построим прямые, задающиеся этими уравнениями.
Построим прямые, задающиеся этими уравнениями.
3) Определим полуплоскости, задаваемые неравенствами. Возьмем произвольную точку, пусть (0; 0). Рассмотрим  , подставим координаты точки :
, подставим координаты точки :  значит, в той полуплоскости, где лежит точка (0; 0),
значит, в той полуплоскости, где лежит точка (0; 0), 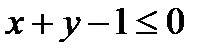 , т.е. полуплоскость, лежащая ниже прямой, является решением первого неравенства. Подставив эту точку (0; 0) во второе уравнение, получим:
, т.е. полуплоскость, лежащая ниже прямой, является решением первого неравенства. Подставив эту точку (0; 0) во второе уравнение, получим:  , т.е. в полуплоскости, где лежит точка (0; 0),
, т.е. в полуплоскости, где лежит точка (0; 0), 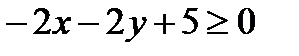 , а нас спрашивали где
, а нас спрашивали где 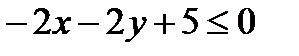 , следовательно, в другой полуплоскости – в той, что выше прямой.
, следовательно, в другой полуплоскости – в той, что выше прямой.
4) Найдем пересечение этих двух полуплоскостей. Прямые параллельны, поэтому плоскости нигде не пересекаются, значит система данных неравенств решений не имеет, несовместна.
Пример 2. Найти графически решения системы неравенств:
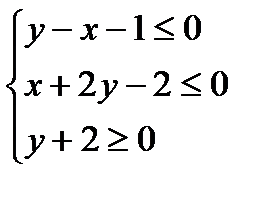
1)  Выпишем уравнения, соответствующие неравенствам:
Выпишем уравнения, соответствующие неравенствам: 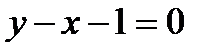 ,
,  ,
, 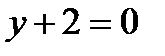
2) Построим прямые, задающиеся этими уравнениями.
Определим полуплоскости, задаваемые неравенствами.
Возьмем произвольную точку, пусть (0; 0).
Определим знаки неравенств в полуплоскостях:
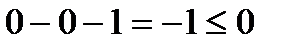 , т.е. полуплоскость ниже прямой;
, т.е. полуплоскость ниже прямой;
 , т.е. полуплоскость ниже прямой;
, т.е. полуплоскость ниже прямой;
 , т.е. полуплоскость выше прямой;
, т.е. полуплоскость выше прямой;
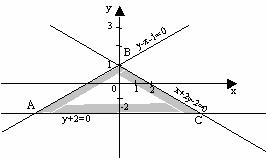
3) Найдем пересечение этих трех полуплоскостей. Пересечением этих трех полуплоскостей будет являться область, являющаяся треугольником.
Пример 3. Найти графически решения системы неравенств:
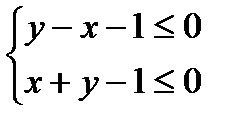
1)  Выпишем уравнения, соответствующие неравенствам:
Выпишем уравнения, соответствующие неравенствам: 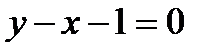 ,
, 
2) Построим прямые, задающиеся этими уравнениями.
3) Определим полуплоскости, задаваемые неравенствами.
Возьмем произвольную точку, пусть (0; 0).
Определим знаки неравенств в полуплоскостях:
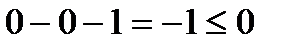 , т.е. полуплоскость ниже прямой;
, т.е. полуплоскость ниже прямой;
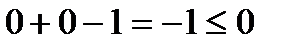 , т.е. полуплоскость ниже прямой;
, т.е. полуплоскость ниже прямой;
4) Найдем пересечение этих двух полуплоскостей. Пересечением этих двух полуплоскостей будет являться угол, с вершиной в точке А(0;1). Эта неограниченная область является решением исходной системы неравенств.
Пример 4. Найти графически решения системы неравенств:
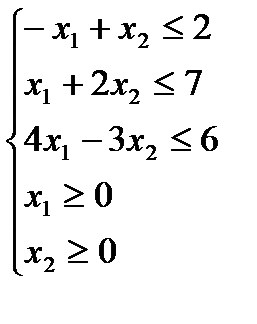
1) Выпишем уравнения, соответствующие неравенствам: 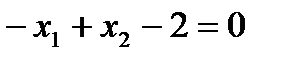 ,
, 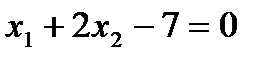 ,
, 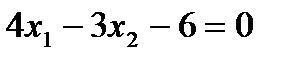 ,
,  .
. 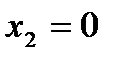
2) 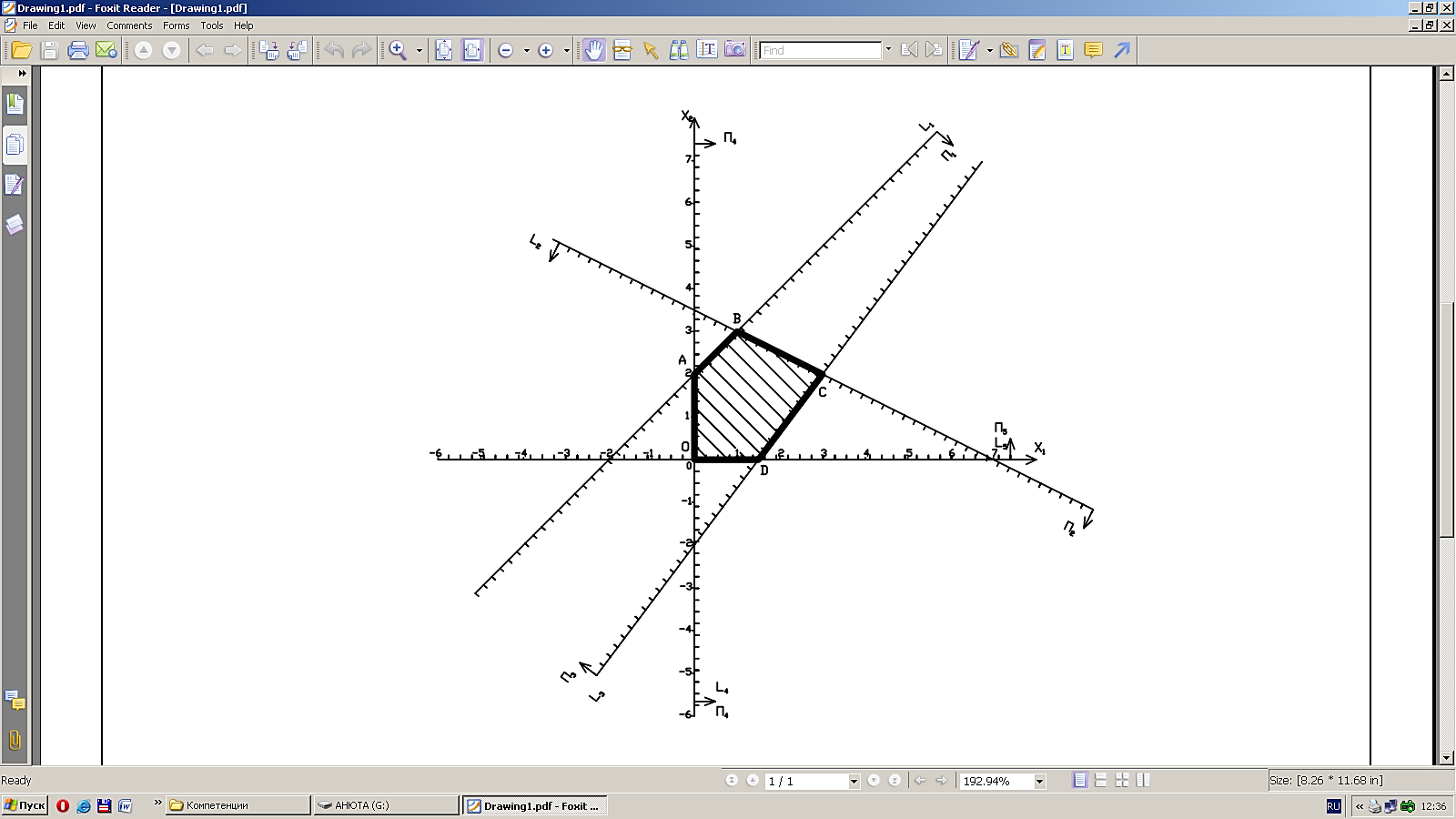 Построим прямые, задающиеся этими уравнениями.
Построим прямые, задающиеся этими уравнениями. 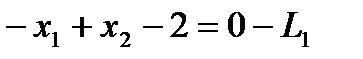 ,
, 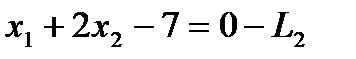 ,
, 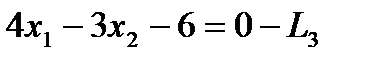 ,
, 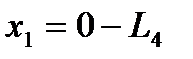 .
. 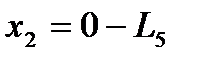
3) Определим полуплоскости, задаваемые неравенствами.
Возьмем произвольную точку, пусть (0; 0).
Определим знаки неравенств в полуплоскостях:
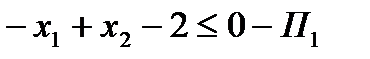 ,
,
 ,
,
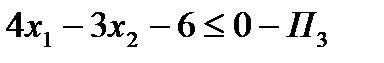 ,
,
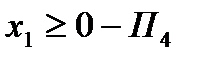 .
.

4) Найдем пересечение этих всех полуплоскостей. В данном случае, множеством решений является пятиугольник OABCD.
Дата добавления: 2014-12-05; просмотров: 3931;
