Неперервність функції

64. Основными критериями оценки деятельности органов прокуратуры по надзору за соблюдением законности при исполнении наказаний, содержании лиц в специальных учреждениях и осуществлении контроля за освобожденными из мест лишения свободы определить:

1) обеспечение верховенства закона при отбывании уголовных наказаний и применении мер процессуального принуждения;

2) неукоснительное соблюдение конституционных прав, свобод и законных интересов задержанного, административно- и следственно-арестованного, осужденного, лица УДООН и поднадзорного;

3) недопущение пыток и других жестоких, бесчеловечных или унижающих достоинство видов обращения и наказания.

65. Прокурорами областей в Департамент к 30 числу каждого месяца направляются информации о результатах проверок и принятых мерах по чрезвычайным происшествиям и всем фактам применения оружия, специальных средств к задержанному, административно- и следственно-арестованному, осужденному, совершения покушения на побег (побега) из специальных и исправительных учреждений, членовредительства и суицида.

66. Ежеквартально проводимые анализы обеспечения надзора за состоянием законности при исполнении наказаний, содержании лиц в специальных учреждениях и осуществлении контроля за освобожденными из мест лишения свободы представляются к обозначенным датам месяца следующего за окончанием квартала:

прокурорами городов и районов в прокуратуры областей и приравненные к ним к 1 числу;

прокурорами областей в Департамент к 5 числу;

Департаментом руководству Генеральной прокуратуры Республики Казахстан к 10 числу.

67. Департаментом и прокурорами областей по итогам работы за полугодие и год обобщается состояние законности отдельно по каждому приоритетному направлению надзора, указанному в подпунктах 1) – 3) пункта 5 настоящей Инструкции, где отмечаются причины и условия, способствующие нарушениям законности, и определяются пути их устранения.

Прокурорами областей информации по обобщениям представляются в Департамент к 5 июля и 5 января.

Департаментом и прокурорами областей обобщения состояния законности использования бюджетных средств, выделяемых на содержание задержанных, административно- и следственно-арестованных, осужденных, а также по вопросу соблюдения законодательства, направленного на адаптацию лиц, освобожденных из мест лишения свободы проводятся по итогам года.

Прокурорами областей в Департамент информации по обобщению данных вопросов представляются соответственно к 1 марта и к 5 января.

68. Департаментом и прокурорами областей на постоянной основе проводится работа по инициированию и внедрению современных методов организации надзора, распространению положительного опыта надзорной деятельности, повышению квалификации сотрудников.

69. Проводится целенаправленная работа по повышению имиджа органов прокуратуры путем освещения в средствах массовой информации состояния законности и правопорядка в специальных и исправительных учреждениях, а также надзорной деятельности прокуроров.

70. Департаментом и прокурорами областей осуществляется взаимодействие с Институтом изучения проблем законности, правопорядка и повышения квалификации кадров органов прокуратуры при Генеральной прокуратуре Республики Казахстан имени С.Ескараева, другими высшими учебными заведениями, научными учреждениями, учеными-юристами по совершенствованию действующего законодательства.

Неперервність функції

План

1. Основні поняття.

2. Властивості неперервних функцій.

3. Розриви функції.

4. Методика дослідження функції на неперервність.

5. Порівняння нескінченно малих величин.

6. Властивості функцій неперервних на відрізку.

1. Основні поняття

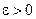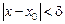Означення(Коші). Функція у = f(x) називається неперервною в точці х₀функцією, якщо ця функція визначена в точці х₀ і для кожного (достатньо малого) числа існує число , таке що при виконується

або

f(x) — неперервна в точці х₀, якщо .

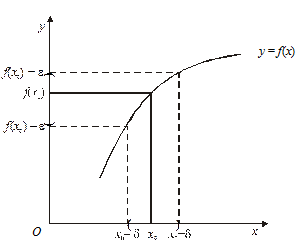
Рис. 1

Функція y = f(x) — неперервна в точці х₀, якщо при будь-якому х з інтервалу значення f(x) лежать у смузі .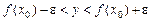

Розглянемо означення неперервності функції, еквівалентні означенню Коші

Означення. Функція y = f(x) називається неперервною в точці х₀, якщо

1) f(x) визначена в точці х₀;

2) границя зліва в точці х₀ дорівнює границі справа в цій точці і дорівнює значенню функції в цій точці (рис. 2):

.

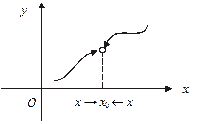
Рис. 2

Означення. Функція у = f(x) називається неперервною в точці х₀, якщо нескінченно малому приросту аргументу відповідає нескінченно малий приріст функції .

Приклад. Довести за означенням, що функції y = x² і y = sin x неперервні в будь-якій точці х₀ Î R.

· 1. Надамо аргументу х₀ Î R приросту Dх, тоді

.

Якщо Dх — нескінченно мала величина, то Dу — також нескінченно мала величина, оскільки коли Dх ® 0, то і Dу ® 0. Отже, y = x²— неперервна функція при будь-якому х₀ Î R.

2. Надамо аргументу х₀ Î R приросту Dх:

Якщо Dх ® 0, то Dу ® 0. Отже, функція y = sin x неперервна функція при будь-якому х₀ Î R.

Означення. Функція у = f(x) неперервна на проміжку (а, b), якщо вона неперервна в кожній точці цього проміжку.

Означення. Функція у = f(x) неперервна на відрізку [а, b], якщо вона неперервна на проміжку (а, b) і неперервна в точці х = а справа і в точці х = b зліва.

Означення. Функція у = f(x) називається неперервною в точці х₀ справа (зліва), якщо правостороння (лівостороння) границя в точці дорівнює значенню функції в цій точці

Теорема 1. Усі елементарні функції неперервні на інтервалах визначеності.

2. Властивості неперервних функцій

Теорема 2. Нехай функції у = f(x) i y = g(x) — неперервні на інтервалі (а, b). Тоді неперервними є також функції:

f(x) ± g(x); f(x) g(x); f(x) / g(x), g(x) ¹ 0.

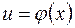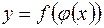Теорема 3. Якщо функція неперервна в будь-якій точці і неперервна в точці , то cкладена функція неперервна в точці .

3. Розриви функції

Означення. Функція у = f(x), яка не є неперервною в точці х₀, називається розривною в цій точці.

Означення. Точка х₀ називається точкою розриву першого роду функції 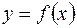, якщо існують скінченні односторонні границі

і при цьому:

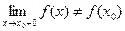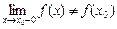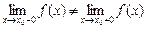або або або або .

Якщо , то величину називають стрибком функції.

Якщ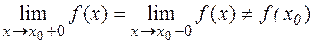о , то – точка усувного розриву.

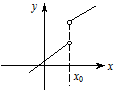
Означення. Точка х₀ називається точкою розриву 2-го роду функції у = f(x), якщо одна із односторонніх границь

не існує або нескінченна.

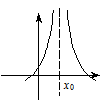
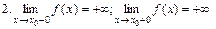
4. Методика дослідження функції у = f(x) на неперервність

1. Знаходимо точку х₀ — «підозрілу» на розрив. Це може бути точка, в якій функція невизначена або змінює закон визначеності.

2. Визначаємо інтервали неперервності функції.

3. Обчислюємо односторонні границі в цій точці

.

4. Робимо висновок згідно з теоремами (якщо такі границі існують), або використовуючи означення точок розриву.

Дослідити на неперервність функцію

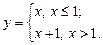
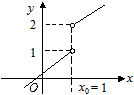
1. Точка х₀ = 1 є «підозрілою» на розрив, оскільки в ній функція змінює закон визначеності (на проміжку (– ¥; 1) маємо у = х, на проміжку (1, +¥) — іншу залежність: у = х + 1).

2. Функція неперервна на проміжках (– ¥; 1) і (1; + ¥).

3. Знаходимо

.

4. 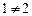, тому за означенням функція 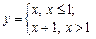має в точці
х = 1 неусувний розрив 1-го роду. – стрибок функції.

Дослідити на неперервність функцію

· 1. Точка х₀ = 0 є «підозрілою» на розрив, оскільки в ній функція змінює закон визначеності.

2. (– ¥; 0) 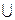(0; + ¥) — множина, де функція неперервна.

3. Знаходимо

1 = 1 =1 — функція неперервна в точці х₀ = 0 за означенням неперервної функції. Отже, інтервалом неперервності функції .

5. Порівняння нескінченно малих величин

Розглянемо функції , , 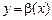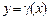і припустимо, що

де а — скінчена точка або нескінченність, тобто , , 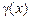— нескінченно малі величини.

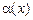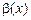Означення. Нескінченно малі величини і називаються нескінченно малими величинами одного порядку, якщо

Означення. Нескінченно мала величина 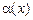називається нескінченно малою величиною вищого порядку, порівняно з 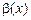, якщо