Означення. Якщо границя не існує, то і називаються непорівнянними нескінченно малими величинами.

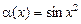Величина — нескінченно мала вищого порядку мализни порівняно з х, оскільки

·

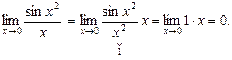Величини і х нескінченно малі при та непорівнянні, оскільки

— не існує. ·

Означення. Нескінченно малі величини і при 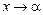називаються еквівалентними, якщо

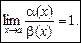
Позначення: Еквівалентність нескінченно малих величин 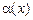і 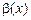позначається a ~ b і означає, що величина a «поводиться як» величина b.

Теорема 1. Для того щоб дві нескінченно малі величини були еквівалентними, необхідно і достатньо, щоб їх різниця була нескінченно малою величиною вищого порядку мализни порівняно з a і b.