Теорема 2. Нескінченно малі величини, які входять до добутку та відношення, можна замінювати їм еквівалентними.
Означення. Нехай 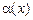 і
і 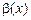 — нескінченно малі величини. У разі, коли
— нескінченно малі величини. У разі, коли
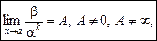
говорять, що нескінченно мала величина b має порядок k відносно нескінченно малої величини a або скорочено: b — величина порядку k. Тоді
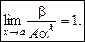
Величина 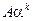 — називається головною частиною нескінченно малої величини b.
— називається головною частиною нескінченно малої величини b.
 Порівняємо нескінченно малі величини
Порівняємо нескінченно малі величини 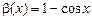 і
і 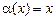 при
при 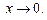
· 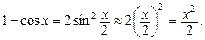
Тоді
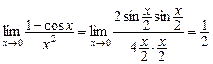 .
.
Отже, величина 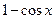 є нескінченно малою другого порядку мализни відносно х. Її головна частина дорівнює
є нескінченно малою другого порядку мализни відносно х. Її головна частина дорівнює 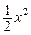 .
.
Шкала еквівалентних нескінченно малих величин
1. 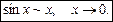
2. 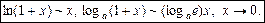
3. 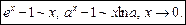
4. 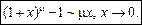
5. 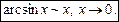
6. 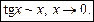
7. 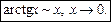
 Знайти границю:
Знайти границю:
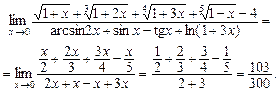
 Зауваження. У виразі, який містить суму та різницю, заміна нескінченно малих величин еквівалентними їм може іноді призвести до помилки.
Зауваження. У виразі, який містить суму та різницю, заміна нескінченно малих величин еквівалентними їм може іноді призвести до помилки.
6. Властивості функцій неперервних на відрізку
Теорема 1. (Больцано-Коші). Нехай функція 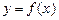 неперервна на відрізку [а; b] і на кінцях його набуває значень різних знаків. Тоді на інтервалі (а; b) знайдеться точка с, в якій функція перетворюється на нуль.
неперервна на відрізку [а; b] і на кінцях його набуває значень різних знаків. Тоді на інтервалі (а; b) знайдеться точка с, в якій функція перетворюється на нуль.
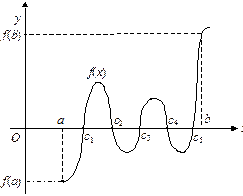
Теорема 2 (Коші). Нехай функція у = f(x) неперервна на відрізку [а; b] і на його кінцях набуває різних значень. Позначимо 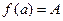 і
і 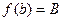 . Тоді при будь-якому С: А < C < B знайдеться точка с із [a, b], така що f(с) = С.
. Тоді при будь-якому С: А < C < B знайдеться точка с із [a, b], така що f(с) = С.
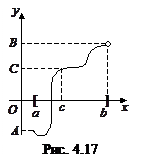 Теорема 3 (Вейєрштрасса). Якщо функція у = f(x) визначена і неперервна на деякому відрізку [а, b], то вона обмежена на цьому відрізку.
Теорема 3 (Вейєрштрасса). Якщо функція у = f(x) визначена і неперервна на деякому відрізку [а, b], то вона обмежена на цьому відрізку.
Теорема 4 (Вейєрштрасса). Функція у = f(x), неперервна на відрізку [а, b], досягає на ньому свого найбільшого та найменшого значення.
7. Рівномірна неперервність
Означення. Функція у = f(x) називається рівномірно неперервною на деякому проміжку І, якщо для довільного 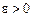 знайдеться
знайдеться 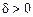 , таке що для будь-яких х1, х2 Î І, які задовольняють умову
, таке що для будь-яких х1, х2 Î І, які задовольняють умову 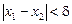 , виконується нерівність
, виконується нерівність 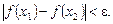
 Розглянемо неперервну функцію
Розглянемо неперервну функцію 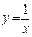 на проміжку (0; 1). Візьмемо довільне
на проміжку (0; 1). Візьмемо довільне 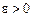 і спробуємо знайти
і спробуємо знайти 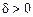 , таке щоб за умови
, таке щоб за умови 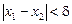 виконувалась нерівність
виконувалась нерівність 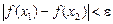 . Дістанемо:
. Дістанемо:
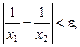 або
або 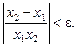
Вираз 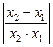 за умови
за умови 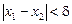 може бути як завгодно великим. Якщо значення
може бути як завгодно великим. Якщо значення 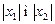 достатньо малі, то нерівність
достатньо малі, то нерівність 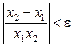 не може виконуватися при всіх
не може виконуватися при всіх 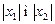 із (0, 1). Отже, ця функція не є рівномірно неперервною.
із (0, 1). Отже, ця функція не є рівномірно неперервною.
 Зауваження. Поняття рівномірної неперервності пов’язане з проміжком, на якому розглядається функція («рівномірно» — це приблизно однаково).
Зауваження. Поняття рівномірної неперервності пов’язане з проміжком, на якому розглядається функція («рівномірно» — це приблизно однаково).
Теорема 5 (Кантора). Якщо функція у = f(x) неперервна на відрізку [а, b], то вона рівномірно неперервна на ньому.
Дата добавления: 2014-11-29; просмотров: 1979;
