Метод двух узлов

Схема на рис. 4.4 имеет два узла.

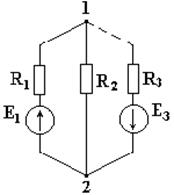
Рис. 4.4

Потенциал точки 2 примем
равным нулю φ 2 = 0. Составим узловое уравнение для узла 1.

,

,

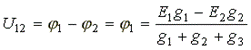где 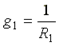, , 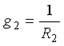- проводимости ветвей.

В общем виде:

.

В знаменателе формулы - сумма проводимостей параллельно включенных ветвей. В числителе - алгебраическая сумма произведений ЭДС источников на проводимости ветвей, в которые эти ЭДС включены. ЭДС в формуле записывается со знаком "плюс", если она направлена к узлу 1, и со знаком "минус", если направлена от узла 1.
После вычисления величины потенциала φ 1 находим токи в ветвях, используя закон Ома для активной и пассивной ветви.