Лабораторна робота № 2. Побудова двофакторної лінійної моделі продуктивності праці
Побудова двофакторної лінійної моделі продуктивності праці
Згідно варіанту завдання (дод. 1) побудувати двофакторну лінійну регресійну модель залежності продуктивності праці (Y, тис.грн./чол.) від втрат робочого часу, (Х1) та коефіцієнту використання потужностей (Х2 ). Необхідно:
1. Знайти параметри моделі.
2. Розрахувати коефіцієнти еластичності, кореляції та детермінації; стандартну та відносну похибки; критерій Фішера.
3. Представити модель на графіку, побудувавши поле кореляції та теоретичну лінію регресії.
4. Зробити загальний економічний аналіз моделі.
Розв’язання.
1. Економічний зміст змінних:
Y – продуктивність праці, тис.грн /чол. (залежна змінна);
Х1 – рівень втрат робочого часу, тис.люд.-год./рік (незалежна змінна);
Х2 – коефіцієнт використання потужностей, % (незалежна змінна).
2. Загальний вид лінійної форми економетричної моделі:
Y = а0 + а1Х1 + а2Х2 + u,
де а0, а1, а2 – параметри моделі; u – залишки, інші невраховані чинники.
2. Вихідні дані для розрахунків та побудови моделі наведені
в табл. 2.1.
Таблиця 2.1
| Спосте-реження | Функція | 1-й аргумент | 2-й аргумент |
| Y | X1 | X2 | |
| 13,1 | 8,3 | 55,8 | |
| 13,4 | 56,1 | ||
| 8,7 | 57,1 | ||
| 12,8 | 8,1 | 60,3 | |
| 14,5 | 7,5 | 61,4 | |
| 14,8 | 6,5 | 62,5 | |
| 15,1 | 70,4 | ||
| 15,4 | 5,9 | 71,7 | |
| 15,9 | 5,4 | 73,7 | |
| 16,3 | 5,1 | 73,7 | |
| 17,4 | 4,3 | 75,8 | |
| 18,1 | 2,1 | 76,7 | |
| 77,9 | |||
| 19,3 | 1,5 | 78,1 | |
| 19,3 | 1,5 | 78,1 |
4. Для визначення коефіцієнтів регресії а0, а1 та а2, складаємо систему нормальних рівнянь:
 а0 N + а1 åX1 + а2 å X2 = å Y
а0 N + а1 åX1 + а2 å X2 = å Y
а0 å X1 + а1 å(X1)2 + а2 å X1 X2 = å Y X1 (2.1)
а0 å X2 + а1 å X1 X2 + а2 å (X2)2 = å Y X2
де n – кількість спостережень, n = 15.
Всі суми обраховуються на основі вихідних статистичних даних
в таблиці 2.2.
5. На основі рівняння 2.1 та обрахованих сум в таблиці 2.2 запишемо для нашого прикладу:
 а0 ×15 + а1 × 80,9 + а2 × 1029,3 = 237,4
а0 ×15 + а1 × 80,9 + а2 × 1029,3 = 237,4
а0 × 80,9 + а1 × 530,07+ а2 × 5260,28 = 1196,84
а0 × 1029,3 + а1 × 5260,28 + а2 × 71690,15 = 16554,47
В результаті розв’язання системи отримуємо значення:
а0 = 18,052, a1 = –0,797, a2 = 0,03.
Таким чином, рівняння регресії буде мати вигляд:
Yрозр = 18,052 – 0,797 × Х1 + 0,03 × Х2 .
6. Визначимо коефіцієнти детермінації для даної моделі.
Для цього обчислимо дисперсії залежної змінної та залишків.
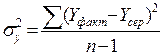 ;
;
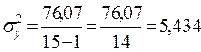 .
.
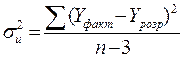 ;
;
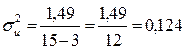 .
.
Таблиця 2.2
| спост | Yфакт | X1 | X2 | Y · X1 | Y · X2 | (X1)2 | (Х2)2 | Х1 · Х2 | Yрозр | (Yфакт–Yрозр)2 | (Yфакт –Yсер)2 |
| 13,1 | 8,3 | 55,8 | 108,7 | 731,0 | 68,9 | 3113,6 | 463,1 | 13,12 | 0,0005 | 7,43 | |
| 13,4 | 8,0 | 56,1 | 107,2 | 751,7 | 64,0 | 3147,2 | 448,8 | 13,37 | 0,0009 | 5,89 | |
| 13,0 | 8,7 | 57,1 | 113,1 | 742,3 | 75,7 | 3260,4 | 496,8 | 12,84 | 0,0249 | 7,99 | |
| 12,8 | 8,1 | 60,3 | 103,7 | 771,8 | 65,6 | 3636,1 | 488,4 | 13,42 | 0,3811 | 9,16 | |
| 14,5 | 7,5 | 61,4 | 108,8 | 890,3 | 56,3 | 3770,0 | 460,5 | 13,93 | 0,3261 | 1,76 | |
| 14,8 | 6,5 | 62,5 | 96,2 | 925,0 | 42,3 | 3906,3 | 406,3 | 14,76 | 0,0016 | 1,05 | |
| 15,1 | 6,0 | 70,4 | 90,6 | 1063,0 | 36,0 | 4956,2 | 422,4 | 15,40 | 0,0881 | 0,53 | |
| 15,4 | 5,9 | 71,7 | 90,9 | 1104,2 | 34,8 | 5140,9 | 423,0 | 15,52 | 0,0134 | 0,18 | |
| 15,9 | 5,4 | 73,7 | 85,9 | 1171,8 | 29,2 | 5431,7 | 398,0 | 15,97 | 0,0056 | 0,01 | |
| 16,3 | 5,1 | 73,7 | 83,1 | 1201,3 | 26,0 | 5431,7 | 375,9 | 16,21 | 0,0074 | 0,22 | |
| 17,4 | 4,3 | 75,8 | 74,8 | 1318,9 | 18,5 | 5745,6 | 325,9 | 16,92 | 0,2349 | 2,48 | |
| 18,1 | 2,1 | 76,7 | 38,0 | 1388,3 | 4,4 | 5882,9 | 161,1 | 18,70 | 0,3557 | 5,17 | |
| 19,0 | 2,0 | 77,9 | 38,0 | 1480,1 | 4,0 | 6068,4 | 155,8 | 18,81 | 0,0352 | 10,07 | |
| 19,3 | 1,5 | 78,1 | 29,0 | 1507,3 | 2,3 | 6099,6 | 117,2 | 19,22 | 0,0069 | 12,06 | |
| 19,3 | 1,5 | 78,1 | 29,0 | 1507,3 | 2,3 | 6099,6 | 117,2 | 19,22 | 0,0069 | 12,06 | |
| S | 237,4 | 80,9 | 1029,3 | 1196,84 | 16554,4 | 530,07 | 71690,1 | 5260,28 | 237,40 | 1,49 | 76,07 |
Коефіцієнт детермінації буде дорівнювати:
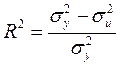 ;
;
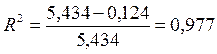 .
.
Отриманий коефіцієнт детермінації R2 = 0,977 свідчить про те, що варіація рівня продуктивності праці на 97,7 % визначається варіацією незалежних змінних Х1 та Х2 і лише 2,3 % змін Y припадає на невраховані чинники.
7. Оцінка точності по середньоквадратичній похибці:
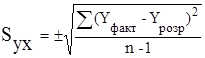
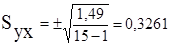
8. Відносна похибка:
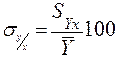
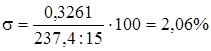
9. Оцінка достовірності по розрахунковому критерію Фішера
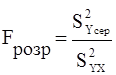
Fрозр. = 76,07: 1,49 = 51,08
Порівнюємо розрахункове значення критерію Фішера з табличним:
F95табл. = 2,5 ;
Fрозр. > F95табл.
Модель приймаємо – припускаємо присутність лінійного зв'язку.
10. Коефіцієнт множинної кореляції
 ;
;
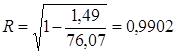 , що свідчить про вельми високий зв’язок між показниками Y та X1 , X2 .
, що свідчить про вельми високий зв’язок між показниками Y та X1 , X2 .
11. Коефіцієнт регресії а1 = – 0,797 показує, що зниження втрат робочого часуна 1 тис. год./рік може привести до роступродуктивностіпраці на 0,797 тис.грн./чол.
Коефіцієнт регресії а2 = 0,03 показує, що підвищення коефіцієнту використання потужності на 1% може привести до росту продуктивності праці на 0,03 тис.грн./чол.
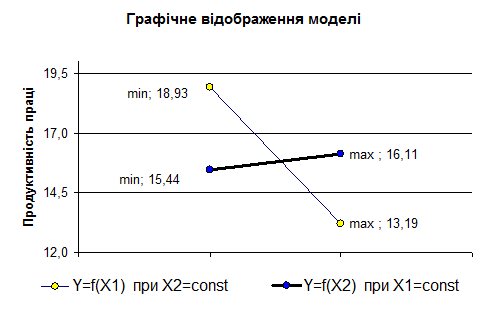
12. Графічне відображення моделі базується на побудові ліній регресії у прямокутних координатах Y-Х1 та Y-Х2. При цьому масштаб необхідно вибрати таким, щоб мінімальні і максимальні значення X1 та X2 співпадали між собою.
| X1 | X2 | Y=f(X1) при X2= const | Y=f(X2) при X1= const | Середнє значення | ||
| X1 | X2 | |||||
| min | 1,50 | 55,80 | 18,93 | 15,44 | 5,39 | 68,62 |
| max | 8,70 | 78,10 | 13,19 | 16,11 |
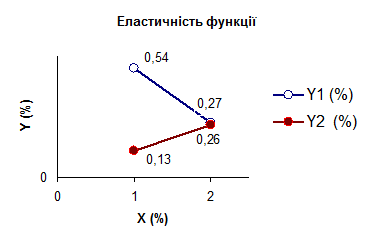
13. Відносна зміна залежної змінної Y в процентах при зміні на 1% аргументів Х1 та Х2 характеризують коефіцієнти еластичності Е1 та Е2, які розраховуються за наступною формулою:
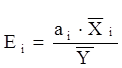
де аі – коефіцієнт регресії при і-тому факторі;
 – середнє значення і-тої незалежної змінної (фактора);
– середнє значення і-тої незалежної змінної (фактора);
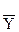 – середнє значення залежної змінної (розрахункове).
– середнє значення залежної змінної (розрахункове).
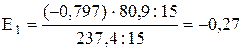
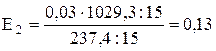
Розраховані коефіцієнти еластичності дають можливість побудувати графік еластичності:
| Х1 (%) | Y1 (%) | Х2 (%) | Y2 (%) |
| –0,27 | 0,13 | ||
| –0,54 | 0,26 |
14. Порівняємо дві моделі (лаб.№1 та лаб. №2)
Коефіцієнти кореляції r = 0,9879 та r = 0,9902 свідчать про те, що залучення другої змінної Х2 збільшує тісноту зв’язку між залежною і факторами. Середньоквадратична похибка зменшилася з 0,3413 до
0,3261 тис.грн./рік. Відносна похибка зменшилась з 2,157% до 2,06%.
15. Висновок.
З аналізу одержаної моделі залежності продуктивності праці від втрат робочого часу і коефіцієнту використання потужності можна зробити висновок, що модель достовірна і може бути використана для кількісного практичного економічного висновку.
На даному підприємстві збільшення продуктивність праці обумовлюється зменшенням втрат робочого часу. Так, при зменшенні втрат робочого часу на кожну 1 тис.год./рік, продуктивність праці збільшиться на 0,797 тис.грн./чол.
При збільшенні коефіцієнту використання потужності на 1% продуктивність праці зросте на 0,03 тис.грн./чол.
Тема: «Методи Побудови множинних економетричних моделей»
Дата добавления: 2014-12-03; просмотров: 3214;
