Лабораторна робота № 1
Побудова лінійних економетричних моделей продуктивності праці
Згідно з вибіркою статистичних даних (дод. 1) потрібно побудувати лінійну економетричну модель залежності продуктивності праці (Y) від втрат робочого часу (Х1). Необхідно:
1. Визначити параметри моделі.
2. Розрахувати коефіцієнти еластичності, кореляції та детермінації; стандартну та відносну похибки; критерій Фішера.
3. Представити модель на графіку, побудувавши поле кореляції та теоретичну лінію регресії.
4. Зробити загальний економічний аналіз моделі.
Розв’язання.
1. Економічний зміст змінних:
Y – продуктивність праці, тис.грн /чол. (залежна змінна);
Х1 – рівень втрат робочого часу, тис.люд.-год./рік (незалежна змінна).
2. Загальний вид лінійної форми економетричної моделі:
Y = а0 + а1 × X + u,
де а0, а1 – параметри моделі; u – залишки, інші невраховані чинники.
3. Вихідні дані для розрахунків та побудови моделі наведені
в табл. 1.1.
Таблиця 1.1
| Спосте- реження | Функція | Перший аргумент |
| Y | Х | |
| 13,1 | 8,3 | |
| 13,4 | ||
| 8,7 | ||
| 12,8 | 8,1 | |
| 14,5 | 7,5 | |
| 14,8 | 6,5 | |
| 15,1 | ||
| 15,4 | 5,9 | |
| 15,9 | 5,4 | |
| 16,3 | 5,1 | |
| 17,4 | 4,3 | |
| 18,1 | 2,1 | |
| 19,3 | 1,5 | |
| 19,3 | 1,5 |
4. Для визначення параметрів моделі а0 та а1 складаємо систему нормальних рівнянь:

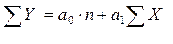
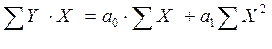 (1.1)
(1.1)
де n – кількість спостережень, n = 15.
Всі суми, що входять у систему, обраховуються на основі похідних статистичних даних (табл. 1.2).
Таблиця 1.2
| Спосте- реження | Y | X | X2 | Y Х | 
| 
| 
|
| 13,1 | 8,3 | 68,89 | 108,73 | 13,24 | 0,01866 | 7,43471 | |
| 13,4 | 64,00 | 107,20 | 13,50 | 0,01080 | 5,88871 | ||
| 8,7 | 75,69 | 113,10 | 12,88 | 0,01435 | 7,99004 | ||
| 12,8 | 8,1 | 65,61 | 103,68 | 13,41 | 0,37802 | 9,16071 | |
| 14,5 | 7,5 | 56,25 | 108,75 | 13,95 | 0,30308 | 1,76004 | |
| 14,8 | 6,5 | 42,25 | 96,20 | 14,84 | 0,00164 | 1,05404 | |
| 15,1 | 36,00 | 90,60 | 15,29 | 0,03463 | 0,52804 | ||
| 15,4 | 5,9 | 34,81 | 90,86 | 15,38 | 0,00062 | 0,18204 | |
| 15,9 | 5,4 | 29,16 | 85,86 | 15,82 | 0,00628 | 0,00538 | |
| 16,3 | 5,1 | 26,01 | 83,13 | 16,09 | 0,04492 | 0,22404 | |
| 17,4 | 4,3 | 18,49 | 74,82 | 16,80 | 0,35892 | 2,47538 | |
| 18,1 | 2,1 | 4,41 | 38,01 | 18,76 | 0,43727 | 5,16804 | |
| 4,00 | 38,00 | 18,85 | 0,02239 | 10,07004 | |||
| 19,3 | 1,5 | 2,25 | 28,95 | 19,30 | 0,00002 | 12,06404 | |
| 19,3 | 1,5 | 2,25 | 28,95 | 19,30 | 0,00002 | 12,06404 | |
| 237,4 | 80,9 | 530,07 | 1196,84 | 237,40 | 1,63162 | 76,06933 |
 – середнє значення Y;
– середнє значення Y; 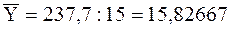 ;
;
 – розрахункове значення Y для моделі.
– розрахункове значення Y для моделі.
5. Якщо підставити в систему рівнянь (1.1) значення n,
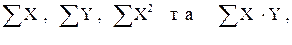 система рівнянь буде мати такий вигляд:
система рівнянь буде мати такий вигляд:

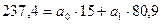
(1.2)
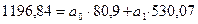
Розв’яжемо цю систему рівнянь відносно невідомих параметрів моделі  та
та 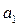 .
.
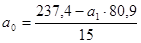 ;
;
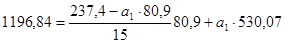 ;
;
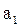 = – 0,89;
= – 0,89;
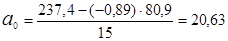 .
.
В результаті розв’язання системи рівнянь отримуємо значення:
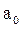 = 20,63,
= 20,63, 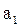 = – 0,89.
= – 0,89.
Отже, економетрична модель продуктивності праці (рівняння регресії) матиме вигляд:
 = 20,63 – 0,89 × Х1 .
= 20,63 – 0,89 × Х1 .
6. Визначимо коефіцієнти детермінації та кореляції для даної моделі.
Для цього обчислимо дисперсії залежної змінної та залишків.
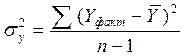 ;
;
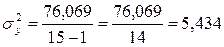
 ;
;
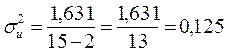 .
.
Коефіцієнт детермінації буде дорівнювати:
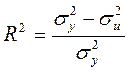 .
.
 .
.
Знаходимо коефіцієнт кореляції:
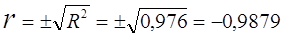 .
.
Коефіцієнт кореляції беремо зі знаком „мінус” оскільки такий знак має коефіцієнт регресії  в моделі.
в моделі.
Рівень коефіцієнта кореляції r= –0,9879 свідчить про тісний обернений зв’язок між продуктивністю праці та втратами робочого часу на підприємстві.
Дата добавления: 2014-12-03; просмотров: 1808;
