ТЕМА 1 5. ЗАКОНЫ ИДЕАЛЬНЫХ ГАЗОВ
15.1 Макроскопические состояния
| Число молей вещества: ν = m/M; ν = V/VM, где m – масса; M - молярная масса; V – объем, VM – молярный объем. |
| Масса одной молекулы: m0= M/NA; m0 = ρ/n, где М – молярная масса, NA= 6,023·1023 моль-1 - число Авогадро; ρ - плотность; n0 - концентрация, определяется из соотношений: n0 = N/V; n = ρ/m0; n = NA/M. |
| Число молекул в данной массе вещества: N = m/m0 = m Na/M. |
| Термодинамическая температура связана с температурой шкалы Цельсия T,K = t°C +273,15; t°C = T,K – 273,15°С |
9.2 Уравнения состояния идеального газа. Изопроцессы
| Уравнения состояния идеального газа (уравнение Менделеева –Клапейрона): для одного моля газа; pVм = RT - для произвольной массы газа: pV = mRT/M; pV = νRT - где Vм - молярный объем; M - молярная масса; m – масса газа; ν = m/M -количество вещества; R – универсальная газовая постоянная |
| Объединенный газовый закон (уравнение Клапейрона): pV/T =const; p1V1/T1 = p2V2/T2 где p –давление газа; V –объем; T – термодинамическая температура |
| Закон Бойля –Мариотта (изотермический процесс): pV = const; p1V1= p2V2 при T=const, m = const |
| Закон Гей-Люссака (изобарический процесс): V =V0(1 + αt) или V/T =const; V1/V2= T1/T2 при p =const, m =const Закон Шарля (изохорический процесс): р= р0(1 + αt) или p/T =const; p1/p2 = T1/T2 при V =const, m =const, где t –температура по шкале Цельсия, V0, p0 –соответственно объем и давление при 00С, коэффициент α =1/273 К-1, p, V, T соответственно давление, объем и термодинамическая температура |
Закон Дальтона для давления смеси n идеальных газов: p = 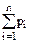 ,
где pi - парциальное давление i -ой компоненты газа ,
где pi - парциальное давление i -ой компоненты газа
|
| Закон Авогадро: при Т0 = 00С =273 К, р0 =1 атм =1,013·105 Па мольный объем любого газа Vм =22,4 л ·моль-1 = 2,24·10-2 м3·моль-1 |
Пример 20. В двух баллонах имеются два газа: водород – Н2 и углекислый газ – СО2. Во сколько раз число молекул одного газа больше числа молекул другого газа, если массы газов одинаковы?
Условие:
М1 =2·10-3 кг/моль;
М2 =44·10-3 кг/моль;
N1/N2 - ?
Решение. В одном моле вещества содержится число молекул, равное числу Авогадро N =6,02·1023 моль-1. Количество вещества водорода ν = m/M1, а в углекислом газе содержиттся число молей ν2 = m/M2. Тогда число молекул водорода N1 = ν1NA = mNA/M1, число молекул углекислого газа N2 = ν2NA = mNA/M2.
Разделив N1 на N2 , получим ответ
N1/N2 = M2/M1 = 44/2 = 22
Пример 21. В баллоне объемом V = 10 л находится гелий под давлением р1 = 1 МПа и при температуре Т1 = 300 К. После того, как из баллона было взято m = 10 г гелия, температура в баллоне понизилась до Т2 = 290 К. Определить давление р2 гелия, оставшегося в баллоне, и изменение внутренней энергии газа.
Условие:
V = 10 л = 10-2 м3;
р1 = 1,0 МПа = 1,0·106 Па;
Т1 = 300 К;
m = 10 г = 1,0·10-2 кг;
Т2 = 290 К;
R = 8,314 Дж/кг·К;
М = 4·10-3 кг/моль;
р2 - ? U -?
Решение. Воспользуемся уравнением Менделеева-Клапейрона, применив его к конечному состоянию газа:
р2V = m2RT2/M, (1)
где m2 – масса гелия в конечном состоянии;
М – молярная масса гелия;
R – универсальная газовая постоянная.
Из уравнения (1) выразим искомое давление
р2 = m2RT2/MV. (2)
Массу m2 гелия выразим через массу m1, соответствующую начальному состоянию, и массу m гелия, взятого из баллона:
m2 = m1 – m. (3)
Массу m1 гелия найдем также из уравнения Менделеева- Клапейрона, применив его к начальному состоянию:
m1 = Mp1V/RT1. (4)
Подставив выражение массы m1 в уравнение (2), а затем выражение m2 в уравнение (1), найдем
p2 = (Mp1V/RT1 – m)RT2/MV, (5)
 .
.
Формула (5) дает единицу давления
[p] = К·Па/К – кг · Дж · К · моль/(кг · моль · м3·К) =
= Па – Дж/м3 = Па – Н·м/м3 = Па.
Вычисления
р2=290·106/300 – 1,0·10-2·8,314·290/(4·10-3·10-2) = 3,64·105 Па.
Внутренняя энергия газа в исходном состоянии
U1 = m1iRT1/2M.
Для газа, оставшегося в баллоне
U2 = m2 iRT2/2M.
Изменение энергии газа
U = U1 – U2 = R(m1 – m2) (T1 – T2)/M = Rm (T1 – T2)/M.
Проверка размерности: [U] = Дж·кг·К·моль/моль·К·кг = Дж.
Ответ: U = 208 Дж.
Дата добавления: 2014-12-02; просмотров: 1187;
