ЗАДАНИЕ 16. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ИДЕАЛЬНОГО ГАЗА
16.1 Идеальный газ как модельная термодинамическая система. Статистические распределения
| Основное уравнение молекулярно-кинетической теории газов: p = n0m<v2кв>/3; p = ρ<v2кв>/3; p =2n<ε>/3; <ε> = m<vкв2>/2, где <vкв> -средняя квадратичная скорость молекул; <ε> - средняя кинетическая энергия поступательного движения молекулы; n0 –концентрация молекул; m - масса одной молекулы; ρ - плотность газа |
| Закон Максвелла для распределения молекул идеального газа по скоростям: f(v) = dN(v)/Ndv = 4π (m0/2πkT)3/2v2exp [ - m0v2/2kT], где функция f(v) распределения молекул по скоростям определяет число молекул dN(v)/N из общего числа молекул, скорости которых лежат в интервале от v до v+dv |
| Барометрическая формула: p = p0 exp [ - Mg (h – h0)/RT]; p = p0exp[ - m0g(h – h0)/kT], где р и р0 – давление газа на высоте h u h0 , M - молярная масса газа, m0 -масса молекулы, R - универсальная газовая постоянная, k - постоянная Больцмана Распределение Больцмана во внешнем центральном поле: n = n0 exp [ -Mgh/RT]; n = n0 exp [-m0gh/kT]; n = n0exp[- Wп/kT] , где n , n0 -концентрация молекул на высоте h и h0=0; Wп - потенциальная энергия молекул в поле тяготения |
| Скорости молекул: наиболее вероятная: vb = (2RT/M)1/2 = (2kT/m0)1/2 = (2p/ρ)1/2 средняя квадратичная: <vкв> =(3RT/M)1/2= (3kT/ m0)1/2 =(3p/ρ)1/2 средняя арифмeтическая: <v> = (8RT/πM)1/2 =(8kT/πm0)1/2= (8p/πρ)1/2 где T - абсолютная температура газа; M - молярная масса газа; m0 – масса одной молекулы; p - давление газа; ρ – плотность газа; R – универсальная газовая постоянная; k – постоянная Больцмана |
| Средняя кинетическая энергия поступательного движения молекулы: <εk> =3kT/2. Средняя полная энергия молекулы: <εk> = ikT/2, где i-число степеней свободы молекул; k – постоянная Больцмана; T –термодинамическая температура одноатомный газ: i =3; двухатомный газ: i=5; многоатомный газ: i =6. |
| Зависимость давления газа от температуры: p = nkT |
Пример 22. Температура окиси азота NO Т =300 К. Определить долю молекул, скорости которых лежат в интервале от v1 = 820 м/с до v2 = 830 м/с
| Условие: Т = 300 К; v1 = 820 м/с; v2 = -830 м/c; ∆N /N - ? | 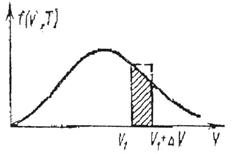
|
Решение. Рассматриваемый газ находится в равновесном состоянии, и согласно Максвеллу, относительное число молекул, скорость которых заключена в интервале от v до v + dv
ΔN/N = f (v, T)dv,
где f (v, T) – функция Максвелла;
dv – настолько малый диапазон скоростей, что в пределах его заведомо f (v, T) = const.
В условии задачи требуется определить долю молекул, скорости которых лежат в диапозоне ∆v = v2 – v1 = 10 м/с.
Если в этом пределе функцию Максвелла можно считать с достаточной точностью постоянной, то искомая величина может быть рассчитана по приближенной формуле
∆N/N = f (v1, N)∆v. (1)
Такое приближение соответствует тому, что на рис. 6 заштрихованная площадь приравнивается к площади прямоугольника с основанием v1 и высотой, равной значению f (v, T).
Следовательно, прежде всего надо найти значения функции Максвелла при v = v1 и v = v2 и выяснить, какую погрешность может дать использование равенства (1).
Функция Максвелла имеет вид
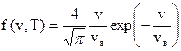 , (2)
, (2)
где vв = (2kT/m0)1/2 = (2RT/M)1/2 - (3)
- наиболее вероятная скорость молекул
Для облегчения расчета найдем сначала наиболее вероятную скорость по равенству (3) vb = 410 м/с.
Тогда согласно (2)
f(v1,T) = 4,03·10-4 c/м f(v2, T) = 3,75·10-4 c/м.
Это означает, что при использовании выражения (23) допускается ошибка относительная величина которой
δf = [f(v1, T) – f (v2, T)]/f (v1, T) = 0,07 = 7%.
Следовательно, с указанной степенью точности можно использовать равенство (2). Тогда доля молекул, скорости которых лежат в заданном интервале
ΔN/N = f (v1, T)∆v = 4,0 ∙ 10-3 = 0,4%.
Дата добавления: 2014-12-02; просмотров: 4211;
