ТЕМА 7. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ. НАПРЯЖЕННОСТЬ И ПОТЕНЦИАЛ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
7.1.Электрический заряд. Закон Кулона
Закон сохранения электрических зарядов
В замкнутой системе: Q = 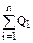 = const = const
|
| Дискретность электрических зарядов: Q = ne, где n= 1, 2... е = ± 1,6 . 10-19 Кл – элементарный электрический заряд |
Закон Кулона:
в векторной форме: 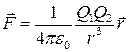 в скалярной форме:
в скалярной форме: 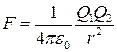 где F12 - сила взаимодействия двух точечных зарядов в вакууме;
r - расстояние между зарядами;
ε0 = 8,85·10-12 Ф·/м - электрическая постоянная
где F12 - сила взаимодействия двух точечных зарядов в вакууме;
r - расстояние между зарядами;
ε0 = 8,85·10-12 Ф·/м - электрическая постоянная
|
Линейная плотность зарядов: 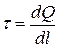 Поверхностная плотность зарядов:
Поверхностная плотность зарядов: 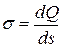 Объемная плотность зарядов:
Объемная плотность зарядов: 
|
7.2. Напряженность и потенциал электростатического поля,
связь между ними. Принцип суперпозиции
Напряженность электростатического поля: 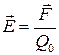 где
где 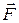 - сила, действующая на точечный положительный заряд Q0, помещенный в данную точку поля.
Потенциал электростатического поля: - сила, действующая на точечный положительный заряд Q0, помещенный в данную точку поля.
Потенциал электростатического поля:  где Wп - потенциальная энергия заряда Q0;
A∞ - работа перемещения заряда из данной точки поля за его пределы.
где Wп - потенциальная энергия заряда Q0;
A∞ - работа перемещения заряда из данной точки поля за его пределы.
|
Принцип суперпозиции:
Напряженность и потенциал результирующего поля, создаваемого системой точечных зарядов, равны соответственно:
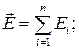  ,
где Е1 и φi - напряженность и потенциал, создаваемый в данной точке поля зарядом Qi. ,
где Е1 и φi - напряженность и потенциал, создаваемый в данной точке поля зарядом Qi.
|
Разность потенциалов между двумя точками электростатического поля:
φ1 – φ2= 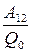 где A12 – работа поля по перемещению заряда между двумя точками поля
где A12 – работа поля по перемещению заряда между двумя точками поля
|
Связь между напряженностью и потенциалом электростатического поля:
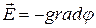 ; φ1 – φ2 = ; φ1 – φ2 = 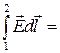  = = 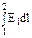 ,
где ,
где 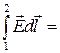 - линейный интеграл напряженности электростатического поля
Однородное электрическое поле: Е = соnst; - линейный интеграл напряженности электростатического поля
Однородное электрическое поле: Е = соnst; 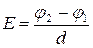 ; Δφ = Ed ; Δφ = Ed
|
Циркуляция вектора напряженности электростатического поля:
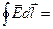  где Е l - проекция вектора E на направление элементарного перемещения dl.
Интегрирование производится по любому замкнутому контуру
где Е l - проекция вектора E на направление элементарного перемещения dl.
Интегрирование производится по любому замкнутому контуру
|
Работа, совершаемая силами электростатического поля при перемещении заряда из точки 1 в точку2: A12 = Q0(φ1 – φ2);
A12 = Q0 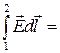 = Q0 = Q0  .
Работа по перемещению точечного заряда Q в поле точечного заряда Q0: .
Работа по перемещению точечного заряда Q в поле точечного заряда Q0:
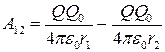 Работа по перемещению заряда в однородном электростатическом поле:
A12 = QE cosα
Работа по перемещению заряда в однородном электростатическом поле:
A12 = QE cosα
|
Пример 9.В вершинах квадрата находятся одинаковые по величине одноименные заряды (рис 9). Определить величину заряда q0, который надо поместить в центр квадрата, чтобы система зарядов находилась в равновесии. Будет ли это равновесие устойчивым?
Условие:
q1 = q2 = q3 = q4 = q;
qo - ?
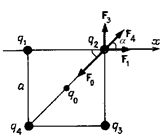 Решение. Рассмотрим силы, действующие на любой из зарядов в вершинах, например на заряд q2 (рис. 9). Со стороны зарядов q1, q2, q3 на него действуют силы F1, F3, F4 соответственно, причем F1 = F3 = kq2/a2 , где а – сторона квадрата, F4 = kq2/2a2. Сила, действующая на заряд q2 со стороны заряда q0 равна F0 = 2kqq0/a2. Условие равновесия заряда имеют вид
Решение. Рассмотрим силы, действующие на любой из зарядов в вершинах, например на заряд q2 (рис. 9). Со стороны зарядов q1, q2, q3 на него действуют силы F1, F3, F4 соответственно, причем F1 = F3 = kq2/a2 , где а – сторона квадрата, F4 = kq2/2a2. Сила, действующая на заряд q2 со стороны заряда q0 равна F0 = 2kqq0/a2. Условие равновесия заряда имеют вид
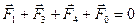 , (1)
, (1)
В проекции на ось х уравнение (1) запишется
F1 + F4cos α – F0 cos α = 0,
или 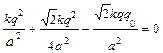 .
.
Откуда q0 = q(1 + 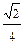 )/
)/ 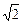 = 0,9 q.
= 0,9 q.
Согласно теореме Ирншоу, система неподвижных точечных зарядов, находящихся на конечном расстоянии друг от друга, не может находиться в состоянии устойчивого равновесия лишь под действием кулоновских сил.
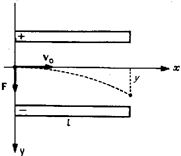
Пример 10.Электрон влетает в плоский воздушный конденсатор параллельно пластинам со скоростью v0 = 1,0·10 6 м/с. Длина конденсатора L=1,0 см, напряженность электрического поля в нем Е =5,0·103 В/м. Найти скорость v электрона при вылете из конденсатора и его смещение у.
Условие:
v0 = 1,0·106 м/с;
L = 1,0 см = 0,01 м;
Е = 5,0·103 В/м;
е = 1,6·10-19 Кл;
m = 9,1·10-31кг;
v - ? y - ?
Решение. Сила тяжести, действующая на электрон, равна Ft = mg = 9,1·10-30 Н.
Кулоновская сила равна F = eE = 8·10-16 Н, т. е. кулоновская сила много больше, чем сила тяжести. Поэтому можно считать, что движение электрона происходит только под действием кулоновской силы.
Запишем для электрона второй закон Ньютона
ma = F, где F = eE.
Направление осей координат показано на рис. 10. Движение электрона вдоль оси х – равномерное со скоростью v0, так как проекция силы F на ось х равна нулю, следовательно время, в течении которого электрон пролетает между пластинами конденсатора t = L/v0.
Движение электрона вдоль оси у – равноускоренное под действием силы F, направленное вдоль этой оси.
Ускорение ау=а=еЕ/m.
Начальная скорость и смещение электрона вдоль оси у равны: vy = 0
 4,4∙10-2 м.
4,4∙10-2 м.
Скорость электрона в момент вылета v, направленная по касательной к траектории его движения равна:
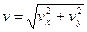 v = (vx2 + vy2)1/2,
v = (vx2 + vy2)1/2,
где vx = v0, vy = at.
Окончательно получаем: 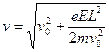 = 8,7·106 м/с.
= 8,7·106 м/с.
Угол между вектором скорости и осью х определяется по формуле
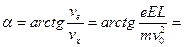 = 83,50.
= 83,50.
ТЕМА 8. ПРИМЕНЕНИЕ ТЕОРЕМЫ ГАУССА К РАСЧЕТУ ЭЛЕКТРОСТАТИЧЕСКИХ ПОЛЕЙ
8.1 Поток вектора напряженности электростатического поля (ПВЭН). Теорема Гаусса
Поток вектора напряженности электростатического поля через элементарную площадку:
d N 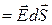 = EdScos α = EndS,
где = EdScos α = EndS,
где 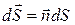 -вектор, модуль которого равен dS , а направление совпадает с нормалью -вектор, модуль которого равен dS , а направление совпадает с нормалью 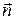 к площади;
En = Ecos α - составляющая вектора к площади;
En = Ecos α - составляющая вектора 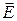 по напрaвлению нормали к площади по напрaвлению нормали к площади
|
Поток вектора электростатического поля через произвольную напряженности поверхность:
NE = 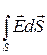 = = 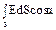 = = 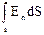
|
Теорема Гаусса для электростатического поля в вакууме:
NE= 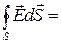 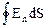 = = 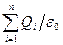 ;
в случае непрерывного распределения зарядов
NE = ;
в случае непрерывного распределения зарядов
NE = 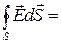 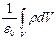 ,
где ε0– электрическая постоянная Qi - алгебраическая сумма зарядов внутри поверхности; n-число зарядов; ρ - объемная плотность зарядов ,
где ε0– электрическая постоянная Qi - алгебраическая сумма зарядов внутри поверхности; n-число зарядов; ρ - объемная плотность зарядов
|
Дата добавления: 2014-12-02; просмотров: 1849;
