Закон сохранения момента импульса. Работа при вращении тела. Кинетическая энергия вращательного движения.
Закон сохранения момента импульса для замкнутой системы
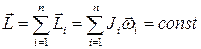
|
| Работа при вращении тела: ΔA = MzΔφ, где Δφ - угол поворота тела; Mz - момент силы относительно оси |
Кинетическая энергия тела, вращающегося вокруг неподвижной оси:
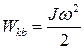 ,
где J– момент инерции тела относительно оси, ω - его угловая скорость
Кинетическая энергия тела, катящегося по плоскости без скольжения: ,
где J– момент инерции тела относительно оси, ω - его угловая скорость
Кинетическая энергия тела, катящегося по плоскости без скольжения:
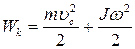 где m– масса тела;
vc - скорость центра масс тела;
J – момент инерции тела относительно оси, проходящей через центр масс;
ω –угловая скорость тела
где m– масса тела;
vc - скорость центра масс тела;
J – момент инерции тела относительно оси, проходящей через центр масс;
ω –угловая скорость тела
|
Пример 8.На скамье Жуковского сидит человек и держит в вытянутых руках гири массой m =10 кг каждая. Расстояние от каждой гири до оси вращения скамьи l1 = 50 см. Скамья вращается с частотой n1 = 1,0 с-1. Как изменится частота вращения скамьи и какую работу A произведет человек, если он сожмет руки так, что расстояние от каждой гири до оси уменьшится до l2 = 20 см. Суммарный момент инерции человека и скамьи относительно оси вращения J =2,5 кг·м2. Ось вращения проходит через центр масс человека и скамьи.
Условие:
m = 10 кг;
l1=50 см = 0,5 м;
n1 =1,0 с-1;
l2 =20 см =0,2 м;
J = 2,5 кг·м2.
n2 - ? А - ?
Решение. Частота вращения скамьи Жуковского изменится в результате действий, производимых человеком при сближении гирь. В системе тел скамья – человек – гири все силы, кроме сил реакции опоры, являются внутренними и не изменяют момента импульса системы. Однако моменты сил реакции опоры относительно вертикальной оси равны нулю. (Для скамьи Жуковского силы трения в оси можно считать отсутствующими.) Следовательно, момент импульса этой системы остается постоянным:
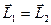 ;
; 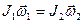 , (1)
, (1)
где J1ω1, J2ω2 - моменты импульса системы соответственно до и после сближения гирь.
Перепишем векторное уравнение (1) в скалярном виде:
J1ω1 = J2ω2. (2)
До сближения гирь момент инерции всей системы: J1 = J0 + 2ml12.
После сближения: J2 = J0 + 2ml22,
где m - масса каждой гири.
Выражая угловую скорость через частоту вращения по формуле ω = 2πn и подставляя ее в уравнение (1) получаем
(J0 + 2ml12)n1 = (J0 + 2ml22)n2.
Откуда 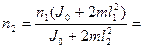 2,3 c-1.
2,3 c-1.
Все внешние силы не создают вращающего момента относительно оси и, следовательно, не совершают работы. Поэтому изменение кинетической энергии системы равно работе, совершенной человеком:
A = W2 - W1 = 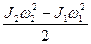 .
.
Учитывая, что ω2 = J1ω1/J2, получаем работу, совершаемую человеком:
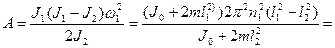 = 190 Дж.
= 190 Дж.
Дата добавления: 2014-12-02; просмотров: 2951;
