ТЕМА 2. ЗАКОНЫ ДИНАМИКИ. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
2.1. Динамика материальной точки и поступательного движения
твердого тела
Импульс материальной точки: 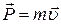 Импульс системы материальных точек:
Импульс системы материальных точек: 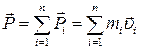
|
Второй закон Ньютона (основное уравнение динамики матеpиальной точки):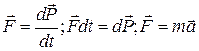 Изменение импульса материальной точки: Δ
Изменение импульса материальной точки: Δ 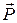 = = 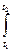 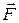 (t)dt. (t)dt.
|
Главный вектор внешних сил: 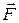 = = 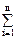 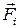 i i
|
Основной закон динамики поступательного движения твердого тела: 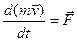
|
Радиус-вектор и координаты центра масс:  x c=
x c= 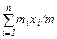 ; yc = ; yc = 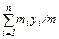 ; zc = ; zc = 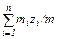 , где , где 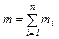 Закон движения центра масс:
Закон движения центра масс: 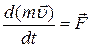
|
Третий закон Ньютона: 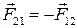
|
Закон сохранения импульса для замкнутой системы:
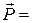 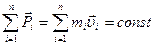 где n -число материальных точек (или тел), входящих в систему.
где n -число материальных точек (или тел), входящих в систему.
|
Пример 3.Автомобиль массой m = 1000 кг движется вверх по наклонной плоскости с уклоном α = 0,1, развивая на пути S = 200 м скорость vк = 54 км/ч. Коэффициент трения μ = 0,05. Определить силу тяги двигателя
Условие:
 m =1000 кг;
m =1000 кг;
S=200 м;
a=0,1 м/с2;
μ=0,05;
v0 =0;
vк =54км/ч = 15м/с;
F - ?
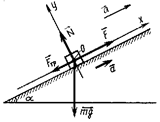
Решение. Автомобиль движется равноускоренно, причем начальная скорость равна нулю. Выберем ось х, расположенную вдоль наклонной плоскости, ось у – перпендикулярно ей (рис. 3).
На автомобиль действует четыре силы: сила тяжести FТ=mg, сила реакции опоры N, сила тяги F и сила трения FТР. Запишем основной закон динамики:
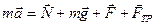 .
.
Это уравнение в проекциях на оси координат
на ось х ma = F – mg sina - FTP,
на ось у 0 = N – mg cosa,
FTP = μ N.
Выразим из этих уравнений силу тяги F
F = mg sina + μmg cosa + ma.
Ускорение на этом участке равно:
a = (vk 2 - v02)/(2s) = vk2/(2s).
Найдем силу тяги двигателя на этом участке:
F = mg sinα + μmg cosα +  = m(g sin α + μg cos α +
= m(g sin α + μg cos α + 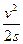 )=
)=
1000(0.98+0,50+0,56) = 2043 Н
Дата добавления: 2014-12-02; просмотров: 1058;
