ФИЗИЧЕСКИЕ ОСНОВЫ КЛАССИЧЕСКОЙ МЕХАНИКИ
ТЕМА 1. КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКи
1.1. Кинематика поступательного движения материальной точки
Положение материальной точки в пространстве определяется с помощью радиус- вектора: 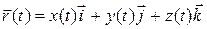 ,
где ,
где 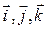 – единичные векторы – орты, направленные по осям прямоугольной системы координат,
x, y, z – координаты точки – единичные векторы – орты, направленные по осям прямоугольной системы координат,
x, y, z – координаты точки
|
Kинематическое уравнение движения материальной точки:
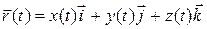 ,
где x(t), y(t), z(t) – функции, выражающие зависимость координат точки от времени t. ,
где x(t), y(t), z(t) – функции, выражающие зависимость координат точки от времени t.
|
Средняя скорость: 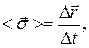 где Δ
где Δ 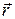 - вектор перемещения за время Δt.
Средняя путевая скорость: - вектор перемещения за время Δt.
Средняя путевая скорость: 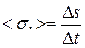 ,
где Δs - путь, пройденный за время Δt.
Мгновенная скорость: ,
где Δs - путь, пройденный за время Δt.
Мгновенная скорость: 
|
Среднее ускорениe: 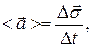 гдеΔ
гдеΔ 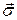 – приращение скорости за время Δt.
Мгновенное ускорение: – приращение скорости за время Δt.
Мгновенное ускорение: 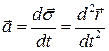 Ускорение при криволинейном движении:
Ускорение при криволинейном движении: 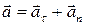 : : 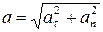 ,
где ,
где 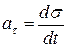 - тангенциальная составляющая ускорения, - тангенциальная составляющая ускорения,
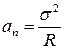 - нормальная составляющая ускорения,
R - радиус кривизны. - нормальная составляющая ускорения,
R - радиус кривизны.
|
Длина пути, пройденного точкой за промежуток времени от t1 до t2:
s = 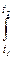 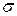 (t)dt .
Координаты матеpиальной точки:X(t) = x(0) + (t)dt .
Координаты матеpиальной точки:X(t) = x(0) + 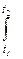 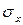 (t)dt . (t)dt .
|
1.2. Кинематика вращательного движения материальной точки
Средняя угловая скорость: 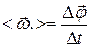 ,
где Δ ,
где Δ 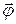 – вектор угла поворота за время Δt .
Мгновенная угловая скорость: – вектор угла поворота за время Δt .
Мгновенная угловая скорость: 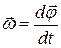 Линейная скорость:
Линейная скорость: 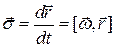 ] ]
|
Среднее угловое ускорение: 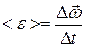 ,
где Δ ,
где Δ 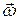 - приращение угловой скорости за время Δt.
Мгновенное угловое ускорение: - приращение угловой скорости за время Δt.
Мгновенное угловое ускорение: 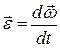 Связь тангенциального ускорения с угловым: at = ε r
Нормальное ускорение:
Связь тангенциального ускорения с угловым: at = ε r
Нормальное ускорение: 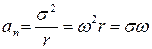 Полное ускорение при вращательном движении:
Полное ускорение при вращательном движении:  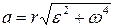 Угол поворота за время t: φ =φ(0) +
Угол поворота за время t: φ =φ(0) + 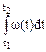
|
1.3. Относительность движения
Cложение перемещений: 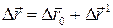 ,
где ,
где 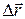 – перемещение точки относительно неподвижной системы отсчета, – перемещение точки относительно неподвижной системы отсчета,  – перемещение точки относительно подвижной системы отсчета, – перемещение точки относительно подвижной системы отсчета,
 – перемещение подвижной системы отсчета относительно неподвижной. – перемещение подвижной системы отсчета относительно неподвижной.
|
Закон сложения скоростей: 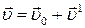 ,
где ,
где 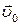 – скорость движения подвижной системы отсчета относительно неподвижной системы отсчета, – скорость движения подвижной системы отсчета относительно неподвижной системы отсчета,
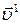 –скорость движения тела относительно подвижной системы отсчета, –скорость движения тела относительно подвижной системы отсчета,
 – скорость движения тела относительно неподвижной системы отсчета. – скорость движения тела относительно неподвижной системы отсчета.
|
Дата добавления: 2014-12-02; просмотров: 932;
