ЗАДАНИЕ 3. СИЛЫ ПРИРОДЫ. МЕХАНИКА СПЛОШНЫХ СРЕД
3.1 Фундаментальные взаимодействия в природе. Упругие свойства тел.
Сила гравитационного взаимодействия: 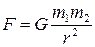 где m1, m2 – массы взаимодействующих материальных точек,
r- расстояние между телами,
G=6,67·10-11Н·м2 ·кг-2- гравитационная постоянная.
где m1, m2 – массы взаимодействующих материальных точек,
r- расстояние между телами,
G=6,67·10-11Н·м2 ·кг-2- гравитационная постоянная.
|
Сила тяжести: 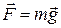 где
где 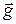 -ускорение свободного падения;
на поверхности Земли: -ускорение свободного падения;
на поверхности Земли: 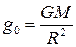 = 9,81 м·с-2,
где M и R - масса и радиус Земли;
на высоте h над поверхностью Земли: = 9,81 м·с-2,
где M и R - масса и радиус Земли;
на высоте h над поверхностью Земли:
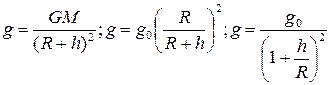 на глубине h от поверхности Земли:
на глубине h от поверхности Земли: 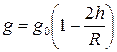
|
Первая космическая скорость вблизи поверхности Земли:
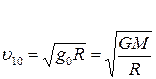 Первая космическая скорость на высоте h от поверхности Земли:
Первая космическая скорость на высоте h от поверхности Земли:
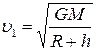 ; ; 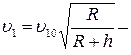 Вторая космическая скорость:
Вторая космическая скорость: 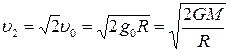
|
Вес тела (сила реакции опоры): P = m(g 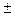 a)
«+» - ускорение направлено вверх;
«—» - ускорение направлено вниз.
Невесомость: P = m(g- a) = 0; g=a
Коэффициент перегрузки: a)
«+» - ускорение направлено вверх;
«—» - ускорение направлено вниз.
Невесомость: P = m(g- a) = 0; g=a
Коэффициент перегрузки: 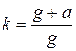
|
Закон Гука для продольного упругого растяжения (сжатия):
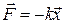 F = k Δ l; σ =εE
где k – коэффициент жесткости,
x – смещение,
Δl=l-l0 – абсолютное удлинение,
lo, l - начальная и конечная длина образца;
σ =F/s – нормальное напряжение;
s – площадь поперечного сечения образца;
ε = Δl/l0 – относительное удлинение;
E - модуль Юнга или модуль упругости. F = k Δ l; σ =εE
где k – коэффициент жесткости,
x – смещение,
Δl=l-l0 – абсолютное удлинение,
lo, l - начальная и конечная длина образца;
σ =F/s – нормальное напряжение;
s – площадь поперечного сечения образца;
ε = Δl/l0 – относительное удлинение;
E - модуль Юнга или модуль упругости.
|
| Сила трения: F = μ N, где μ – κоэффициент трения, N - сила реакции опоры |
Сила сопротивления при движении тела в жидкости и газе соответственно при малых и больших скоростях: F= - β1 v; F = - β2 v2,
где β1, β2 - коэффициенты сопротивления движению,
v - относительная скорость движения.
В случае турбулентного движения при не очень больших скоростях лобовое сопротивление: 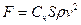 ,
где Сх – коэффициент лобового сопротивления, зависящий от формы тела и числа Рейнольдса,
S- площадь проекции тела на плоскость, перпендикулярную скорости потока,
ρ - плотность среды.
Число Рейнольдса ,
где Сх – коэффициент лобового сопротивления, зависящий от формы тела и числа Рейнольдса,
S- площадь проекции тела на плоскость, перпендикулярную скорости потока,
ρ - плотность среды.
Число Рейнольдса 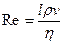 где l - величина, характеризующая линейные размеры обтекаемого тела
где l - величина, характеризующая линейные размеры обтекаемого тела
|
3.2 Механика сплошных сред
| Гидростатическое давление столба жидкости: P = ρgh, где ρ – плотность жидкости. Закон Архимеда: Fa= ρgV, где Fa–выталкивающая сила; V - объем вытесненной жидкости |
| Уравнение неразрывности струи: Sv = const, где S- площадь поперечного сечения трубки тока; v –скорость движения жидкости |
| Уравнение Бернулли для стационарного течения идеальной жидкости: ρv2/2 + ρgh + P = const, где P– статическое давление жидкости для определенного сечения трубки тока; v-скорость жидкости для этого сечения; ρv2/2 - динамическое давление жидкости этогo сечения; h -высота на которой располагается сечение; ρgh - гидростатическое давление, ρ – плотность жидкости |
Скорость истечения жидкости из малого отверстия в открытом сосуде: 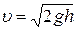 ,
где h – глубина, на которой находится отверстие относительно уровня жидкости в сосуде ,
где h – глубина, на которой находится отверстие относительно уровня жидкости в сосуде
|
Сила внутреннего трения между слоями текущей жидкости: 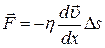 где η - коэффициент динамической вязкости жидкости;
где η - коэффициент динамической вязкости жидкости;
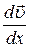 - градиент скорости; - градиент скорости;
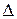 S - площадь соприкасающихся слоев S - площадь соприкасающихся слоев
|
| Сила сопротивления, действующая на шарик, равномерно движущийся в вязкой среде (формула Стокса): F = - 6πηrv, где r -радиус шарика; v - скорость его движения |
Пример 4.На горизонтальной платформе шахтной клети стоит человек массой m = 60 кг. Определить силу давления человека на платформу: 1) при ее подъеме с ускорением
а1 = 3 м/с2; 2) при равномерном подъеме и спуске; 3) при спуске с ускорением а3 = 9,8 м/с2.
 Условие:
Условие:
m=60 кг;
а1=3 м/с2;
v2=const, a2=0;
а3=9,8 м/с;
F1- ? F2 - ? F3 - ?
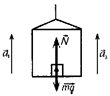
Решение. На человека, стоящего на платформе шахтной клети действуют две силы: сила тяжести mg и сила реакции опоры N. Согласно второму закону Ньютона:
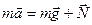 .(1)
.(1)
Согласно третьему закону Ньютона сила давления человека на платформу равна силе реакции опоры:
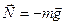 NN = F (2)
NN = F (2)
1. Согласно рис. 2 запишем уравнение (1) в проекции на ось У
ma1 = N1 – mg
Учитывая (2) получим
F1 = N1 = m (g + a1), F1 = 783 H.
2. При равномерном движении шахтной клети а2 = 0 и, следовательно, сила давления человeка на платформу равна силе тяжести: F2 = N2 = mg.
3. При спуске платформы с ускорением, направленным вниз уравнение движения платформы имеет вид ma3 = mg – N3.
Откуда сила давления человека на платформу: F3 = N3 = =m(g – a3).
Учитывая, что а3 = g имеем F3 = 0 .
Следоватeльно, человек не давит на платформу.
Пример 5.Каким был бы период обращения ИСЗ на круговой орбите, если бы он был удален от поверхности Земли на расстояние, равное земному радиусу (R = 6400 км).
Условие: h = R = 6370 км;
Т - ?
Решение. Период обращения ИСЗ по круговой орбите равен:  .
.
Для определения скорости спутника учтем, что при его движении по круговой орбите на спутник действует только сила притяжения Земли Ft, сообщающая ему нормальное ускорение:
Ft = Fn; 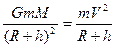
где G – гравитационная постоянная, m – масса спутника, M – масса Земли.
Отсюда скорость спутника равна
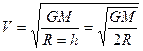
Учитывая, что 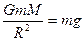
где g – ускорение силы тяжести на поверхности Земли, получаем 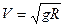
Подставляя это значение скорости в формулу периода, найдем, что
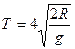 = 14360 c = 3 ч 59 мин.
= 14360 c = 3 ч 59 мин.
Пример 6.Стальная прoвoлока сечением S= 3 мм2 под действием растягивающей силы, равной F = 4 . 104 Н имеет длинy L1 = 2 м. Определить абсолютное удлинение проволоки при увеличении растягивающей силы на F1 = 104 Н. Модуль Юнга стали Е =2 . 1011 Па.
Условие:
Е = 2·1011 Па;
S= 3 мм2 =3·10-6 м2;
L1 = 2 м;
F = 4·104 Н;
F1 =1,0·104 Н;
ΔL2 - ?
Решение. Для того чтобы найти абсолютное удлинение проволоки при увеличенной растягивающей силе, необходимо узнать ее первоначальную длину L. Из закона Гука
F = εE = E(L1 – L)S/L
находим L = EL1S/(F +ES).
При увеличении растягивающей силы на величину F1
F + F1 = EΔL2S/L.
Откуда ΔL2 = (F + F1)L/ES.
Заменив L выражением, записанным выше, получаем
ΔL2 = (F + F1)L1/(F + ES).
Подставив данные, находим: ΔL2 = 0, 16 м.
Дата добавления: 2014-12-02; просмотров: 1297;
