Определение усилий в ригеле
Расчетная схема ригеля – однопролетная шарнирно опертая балка пролетом 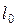 . Вычисляем значения максимального изгибающего момента М и максимальной поперечной силы Q от полной расчетной нагрузки:
. Вычисляем значения максимального изгибающего момента М и максимальной поперечной силы Q от полной расчетной нагрузки:
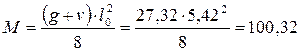 кН·м;
кН·м;
 кН.
кН.
3.3 Расчет прочности ригеля по сечению, нормальному
к продольной оси
Определяем высоту сжатой зоны  , где
, где  мм – рабочая высота сечения ригеля;
мм – рабочая высота сечения ригеля;  - относительная высота сжатой зоны, определяемая в зависимости от коэффициента
- относительная высота сжатой зоны, определяемая в зависимости от коэффициента 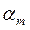 .
.
Расчетный коэффициент:
 .
.
Согласно таблице А.5 приложения при 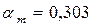 определяем значения коэффициентов
определяем значения коэффициентов 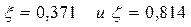 .
.
Высота сжатой зоны 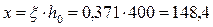 мм, что не более высоты узкой части сечения ригеля. Следовательно, граница сжатой зоны проходит в узкой части сечения, и поэтому расчетным будет прямоугольное сечение.
мм, что не более высоты узкой части сечения ригеля. Следовательно, граница сжатой зоны проходит в узкой части сечения, и поэтому расчетным будет прямоугольное сечение.
Граничная относительная высота сжатой зоны определяется по формуле:
 , (3.2)
, (3.2)
где 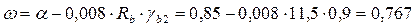 ;
;  МПа.
МПа.

Так как 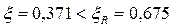 , то площадь сечения растянутой арматуры определяется по формуле:
, то площадь сечения растянутой арматуры определяется по формуле:

 мм2.
мм2.
Из условий конструирования двух каркасов, содержащих по два стержня каждый, принимаем по сортаменту 4Æ20 A-II (А300) с 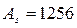 мм2, что больше требуемой.
мм2, что больше требуемой.
3.4 Расчет прочности ригеля по сечениям, наклонным к продольной оси
Расчет производится рядом с подрезкой в месте изменения сечения ригеля.
Поперечная сила на грани подрезки на расстоянии 10 см от торца площадки опирания определяется по формуле:
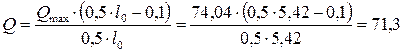 кН.
кН.
Проверяем условие обеспечения прочности по наклонной полосе между наклонными трещинами по формуле:
 , (3.3)
, (3.3)
где  , но не более 1,3; где
, но не более 1,3; где 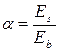 и
и 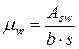 .
.
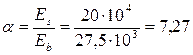 .
.
Ориентировочно принимаем коэффициент поперечного армирования  . Отсюда
. Отсюда 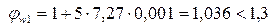 .
.
Коэффициент 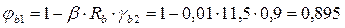 ,
,
где  для тяжелого бетона.
для тяжелого бетона.
Делаем проверку по формуле (3.3):
 .
.
Следовательно, размеры поперечного сечения ригеля достаточны для восприятия нагрузки.
Проверяем необходимость постановки расчетной поперечной арматуры исходя из условия:
 , (3.4)
, (3.4)
где  - коэффициент, принимаемый для тяжелого бетона;
- коэффициент, принимаемый для тяжелого бетона; 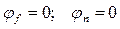 , т.к. рассматривается ригель прямоугольного сечения без предварительно напряженной арматуры.
, т.к. рассматривается ригель прямоугольного сечения без предварительно напряженной арматуры.
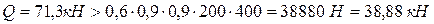 .
.
Вывод: Условие не удовлетворяется, конструктивного армирования недостаточно. Поперечная арматура необходима по расчету.
Расчет для обеспечения прочности по наклонной трещине производится по наиболее опасному наклонному сечению из условия:
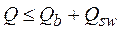 . (3.5)
. (3.5)
Поперечное усилие, воспринимаемое бетоном, равно:
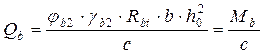 . (3.6)
. (3.6)
Для тяжелого бетона  .
.
Определяем максимальную длину проекции опасного наклонного сечения на продольную ось ригеля  :
:
 мм.
мм.
Поперечное усилие, воспринимаемое хомутами, составляет:
 кН.
кН.
Приняв 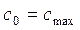 усилия в хомутах на единицу длины ригеля равны:
усилия в хомутах на единицу длины ригеля равны:
 Н/мм.
Н/мм.
При этом должно выполняться условие:
 Н/мм.
Н/мм.
Так как 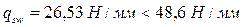 , принимаем
, принимаем  .
.
Определяем длину проекции опасной наклонной трещины на продольную ось ригеля:
 мм.
мм.
и принимаем в пределах 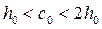 , а так же с0 < с.
, а так же с0 < с.
Поскольку  принимаем
принимаем 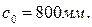
Уточняем величину  :
:
 кН.
кН.
При этом 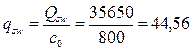 Н/мм.
Н/мм.
Так как  , принимаем
, принимаем  .
.
Из условия сварки с продольной арматурой максимального диаметра (dmax=20 мм) принимаем поперечную арматуру Æ8 A-II (А300).
При двух каркасах 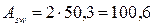 мм2. Шаг поперечных стержней на приопорных участках:
мм2. Шаг поперечных стержней на приопорных участках:
 мм.
мм.
Из условия обеспечения прочности наклонного сечения в пределах участка между хомутами максимально возможный шаг поперечных стержней:
 мм.
мм.
Кроме того, по конструктивным требованиям поперечная арматура устанавливается:
- на приопорных участках, равных 1/4 пролета, при  мм:
мм:
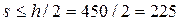 мм и
мм и  мм;
мм;
- на остальной части пролета при  мм с шагом:
мм с шагом:
 мм и
мм и 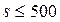 мм.
мм.
Окончательно принимаем шаг поперечных стержней:
- на приопорных участках длиной ¼ пролета 1,5 м s = 150 мм;
- на приопорных участках в подрезке s = 75 мм;
- на остальной части пролета s = 300 мм.
3.5 Построение эпюры материалов
Продольная рабочая арматура в пролете 4Æ20 A-II (А300) с  мм2. Площадь этой арматуры определена из расчета на действие максимального изгибающего момента в середине пролета. В целях экономии арматуры по мере уменьшения изгибающего момента к опорам два стержня обрываются в пролете, а два других доводятся до опор. Если продольная рабочая арматура разного диаметра, то до опор доводят два стержня большего диаметра.
мм2. Площадь этой арматуры определена из расчета на действие максимального изгибающего момента в середине пролета. В целях экономии арматуры по мере уменьшения изгибающего момента к опорам два стержня обрываются в пролете, а два других доводятся до опор. Если продольная рабочая арматура разного диаметра, то до опор доводят два стержня большего диаметра.
Место теоретического обрыва верхних стержней определяется построением «эпюры материалов», которую можно считать эпюрой несущей способности ригеля при фактически применяемой арматуре.
Площадь рабочей арматуры As(4Æ20)=1256 мм2.
Определяем изгибающий момент, воспринимаемый ригелем с полной запроектированной арматурой 4Æ20 A-II (А300) по формуле:
 , (3.7)
, (3.7)
где 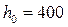 мм.
мм.
Из условия равновесия 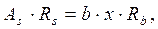 где
где  :
:
 .
.
По приложению А.5 находим  .
.
Изгибающий момент по формуле (3.7) равен:
М(4Æ20) = 270·1256·0,794·400 = 107704512 Н·мм = 107,704 кН·м.
Изгибающий момент, воспринимаемый сечением, больше изгибающего момента, действующего в сечении:
107,704 кН·м > 100,32 кН·м.
До опоры доводятся 2Æ20 A-II (А300) с 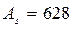 мм2.
мм2.
Вычисляем изгибающий момент, воспринимаемый сечением ригеля с арматурой 2Æ20 A-II (А300):
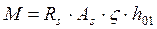 , (3.8)
, (3.8)
где  мм.
мм.
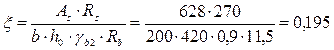 .
.
По приложению А.5 принимаем 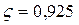 .
.
М(2Æ20) = 270·628·0,925·420 = 65874060 Н·мм = 65,874 кН·м.
Графически по эпюре моментов (рисунок 3.2) определяем место теоретического обрыва стержней 2Æ20 A-III . Эпюра моментов для этого должна быть построена точно с определением значений изгибающих моментов в 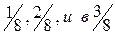 пролета.
пролета.
Изгибающий момент в 1/8 пролета равен:
 .
.
Изгибающий момент в 1/4 пролета равен:
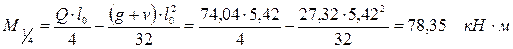 .
.
Изгибающий момент в 3/8 пролета равен:
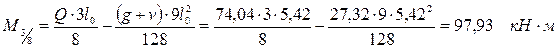 .
.
Откладываем на этой эпюре М(2Æ20)= 65,78 кН·м в масштабе. Точка пересечения прямой с эпюрой называется местом теоретического обрыва арматуры.
Момент, воспринимаемый сечением ригеля с арматурой 2Æ20 A-II (А300), также откладывается в масштабе на эпюре М.
Длина анкеровки w обрываемых стержней определяется по следующей зависимости:
 . (3.9)
. (3.9)

Рисунок 3.2 – Эпюра моментов, материалов и поперечной силы
Поперечная сила Q определяется графически в месте теоретического обрыва, в данном случае Q = 46,74 кН.
Поперечные стержни Æ8 A-III(из условия свариваемости с продольными стрежнями диаметром 20 мм) с  мм2 в месте теоретического обрыва имеют шаг 150 мм.
мм2 в месте теоретического обрыва имеют шаг 150 мм.
 ;
;
 мм
мм  мм.
мм.
Принимаем 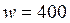 мм.
мм.
Окончательно принимаем длину обрываемых стержней 2Æ20 А-III (А400) 4080 м, которая находится графически путем точных построений.
Дата добавления: 2014-12-02; просмотров: 4604;
