Этапы процесса проектирования

Итак, по результатам расчета можно судить о работоспособности варианта конструкции, который был предложен в результате первоначального процесса конструирования. Если полученные с помощью расчета параметры конструкции будут признаны неудовлетворительными, должен последовать возврат к этапу конструирования с тем, чтобы найти более эффективные конструктивные решения.

Таким образом, процесс проектирования представляет собой итерационный процесс, состоящий из последовательно повторяющихся этапов конструирования и расчета.

Процесс проектирования конструкции грубо можно разделить на две стадии (рис.1.1).

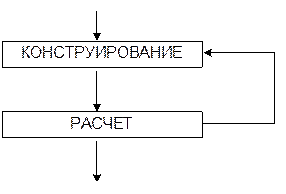
Рис. 1.1

Например, при проектировании рамы промышленного здания, на этапе конструирования может быть принято решение о перекрытии пролета балкой. В результате расчета может быть установлена неэффективность такого решения. В этом случае может быть рассмотрен новый вариант конструкции, в котором пролет перекрывается фермой (рис. 1.2). Расчет может показать неэффективность и такого конструктивного решения, после чего вновь потребуется возврат на этап конструирования и т.д.

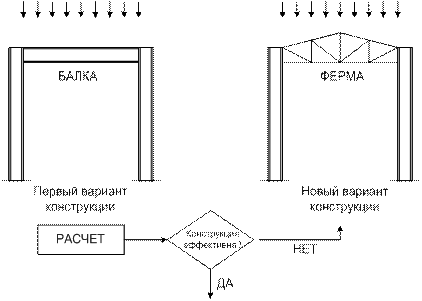
Рис. 1.2

1.4 Расчетные дисциплины, составляющие «Механику деформируемого твердого тела»

В широком смысле все расчетные дисциплины, а именно: сопротивление материалов, строительная механика, теория упругости, теория пластичности, теория ползучести, а также механика разрушения занимаются разработкой методов моделирования механических процессов, имеющих место в реальных конструкциях. Чем сложнее подлежащий моделированию реальный физический процесс, тем более сложным являются математические зависимости, его описывающие.

Исходя из характера работы конструкции, необходимо определить достаточную степень точности моделирования реальных физических процессов. В большинстве случаев это позволяет сильно упростить уравнения модели. Упрощение уравнений достигается введением некоторых дополнительных упрощающих положений и гипотез. Так, в сопротивлении материалов, уравнения которого можно считать наиболее простыми, используются: закон Гука, гипотеза плоских сечений, принцип Сен-Венана и т.п. Формулы теории упругости получены при меньшем числе упрощающих положений. Не используется, например, гипотеза плоских сечений. Расчет ряда конструкций не может быть признан соответствующим реальности, если при его проведении не учитывались пластические деформации. Для их учета следует отказаться от закона Гука, что приводит к еще более сложным соотношениям теории пластичности и ползучести.

Уравнения, составляющие математическую модель (рис. 1.3), можно разбить на три группы:

· статические уравнения (уравнения равновесия)

· геометрические уравнения (уравнения неразрывности деформаций)

· физические уравнения (уравнения, связывающие внутренние силы или напряжения с деформациями тела).

Рис. 1.3