ФОРМАЛЬНОЕ ОПРЕДЕЛЕНИЕ АБСТРАКТНОЙ СИСТЕМЫ
Введем, прежде всего, следующие исходные понятия:
1. Системой (абстрактной) S называется отношение над абстрактными множествами Х и У:
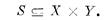
2. Если S — функция, S: Х -> У, мы будем называть систему функциональной.
Для простоты мы будем писать просто “система” без указания на то, является ли она функциональной, когда это свойство несущественно или когда оно вытекает из контекста.
Входящие в определение системы множества Х и У характеризуют входные и выходные объекты и называются соответственно входным и выходным множествами, а их элементы — входами и выходами. Таким образом, представление системы в виде отношения есть представление в форме “вход — выход”. Входы функциональной системы могут рассматриваться как причины, а выходы как следствия;
Рассмотрим разностное уравнение
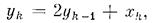 (1)
(1)
описывающее некоторые наблюдения, которые проводятся в дискретные моменты времени Т = {1, 2. .... п}. Для заданного начального условия y0 каждому набору из п чисел х = (xa= 1,..., xn RÎ) n соответствует единственный набор у = (y1, .... yn RÎ) n, который удовлетворяет уравнению (1) для каждого k = 1, .... п. Таким образом, определено отображение Sa: Rn->Rn, такое, что для всех х из Rn-образ у = Sa (x) является единственным решением уравнения (1) при заданном начальном условии у0. Если допустимые начальные условия образуют множество Ya= 0 RÍ R, мы получаем отношение S Ín * Rn SÈ, причем S = a RÍ. Таким образом, приведенное выше уравнение описывает и общем случае систему S n* Rn и, в частности, определяет функциональную систему Sa, когда задано начальное условие y0.a=
Рассмотрим простую динамическую систему:
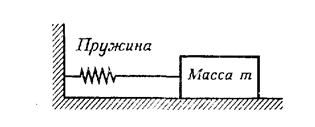
Обозначим коэффициент упругости невесомой пружины через k, смещение тела массы т из положения равновесия в момент времени t — через у'' (t), а внешнюю силу, действующую на тело в момент времени t, через х (t). Предположим, что трение отсутствует. Тогда связь между х (t} и у (t) задается следующим дифференциальным уравнением:
my'' (t) = x(t) - ky(t) (2)
TÎ Y, такое, что для каждого t Î Х соответствует единственным образом определённое у Î = (у (0), у' (0)) каждому х a). Пусть Х — множество всех интегрируемых вещественных функций, определенных на Т, а Y — множество всех вещественных функций на Т. Тогда для заданных начальных условий ¥Предположим, что мы наблюдаем х (t) и у (t) в интервале времени Т= [0,
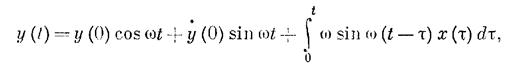
где w= (k/m)1/2. Таким образом, это уравнение описывает однозначное отображение Sa: Х —> У.
R * R, то данная система представляется отношениемÍ Если множеством допустимых начальных условий является A
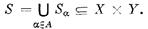
Дата добавления: 2015-01-02; просмотров: 865;
