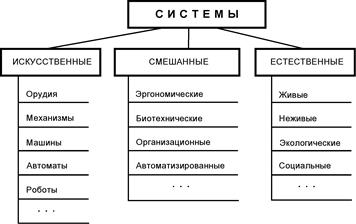
Классификация систем по их происхождению

Часто оказывается необходимым провести разграничение внутри одного класса, не отказываясь тем не менее от общности в его рамках. Так появляются подклассы, что приводит к многоуровневой, иерархической классификации. При необходимости такая классификация может быть продолжена без изменения ее верхних уровней. Если полнота классификации первого уровня логически ясна, то второй уровень на полноту не претендует. Разбиение искусственных систем соответствует рассуждениям, приведенным в § 1.2; неполнота на этом уровне связана, например, с еще незавершенным развитием систем искусственного интеллекта. В качестве примеров подклассов смешанных систем можно привести эргономические системы (комплексы машина – человек-оператор), биотехнические (системы, в которые входят живые организмы и технические устройства) и организационные системы (состоящие из людских коллективов, которые оснащены необходимыми средствами). Классификация естественных систем ясна из рис. 4.1; ее неполнота очевидна. Например, не решен окончательно вопрос о том, куда следует отнести вирусы: к живым или неживым системам.

51.ТИПЫ ПЕРЕМЕННЫХ СИСТЕМЫ
Рассмотрим их подробнее. На рис. 4.3 приведена трехуровневая классификация систем по типу входных (X), выходных (Y) и внутренних (Z) (если описание ведется не на уровне “черного ящика”) переменных. Принципиально разных подходов требуют переменные, описываемые качественно и количественно, что и дает основание для первого уровня классификации. Для полноты введен третий класс, к нему отнесены системы, у которых часть переменных носит качественный характер, а остальные являются количественными. На следующем уровне классификации систем с качественными переменными различаются случаи, когда описание ведется средствами естественного языка, и случаи, допускающие более глубокую формализацию. Второй уровень классификации систем с количественными переменными вызван различиями в методах дискретной и непрерывной математики, что и отражено в названиях вводимых классов; предусмотрен и случай, когда система имеет как непрерывные, так и дискретные переменные. Для систем со смешанным количественно-качественным описанием переменных второй уровень является объединением классов первых двух ветвей и на рисунке не приводится. Третий уровень классификации одинаков для всех классов второго уровня и изображен только для одного из них. Различия между классами третьего уровня будут рассмотрены в гл. 6.

52.ТИПЫ ОПЕРАТОРОВ СИСТЕМЫ

Следующая классификация (рис. 4.4) – по особенностям оператора S системы, т.е. классификация типов связей между входными и выходными переменными. Материал для этого типа классификации дает § 3.7. На первом уровне расположены классы систем, отличающиеся степенью известности оператора S. Ветвь “черного ящика” на этом уровне кончается: S считается вообще неизвестным. Чем больше сведений об S мы имеем, тем больше различий можно рассмотреть и тем более развитой окажется классификация. Например, информация об S может носить настолько общий характер, что модель нельзя привести к параметризованной функциональной форме. Так, может быть известно, что в соотношении Y = S(X) функция S непрерывна, монотонна или симметрична; отсюда не следует никаких конкретных выводов о функциональном виде этой зависимости.

53.ТИПЫ СПОСОБОВ УПРАВЛЕНИЯ
Первый уровень классификации определяется тем, входит ли управляющий блок в систему или является внешним по отношению к ней; выделен также класс систем, управление которыми разделено и частично осуществляется извне, а частично – внутри самой системы.
Независимо от того, включен ли в систему и вынесен ли из нее управляющий блок, можно выделить четыре основных типа (способа) управления, что и отражено на втором уровне классификации (рис. 4.5). Эти способы различаются в зависимости от степени известности траектории*, приводящей систему к цели, и возможности управляющей системы удерживать управляемую систему на этой траектории.
Первый (простейший) случай имеет место тогда, когда нужная траектория известна точно, а следовательно, априори известно и правильное программное управлениеu₀(t). В таком случае это управление можно осуществлять, не обращая внимание на развитие событий; ведь и так известно, как они должны (и будут) развиваться. Стрельба из ружья, работа ЭВМ по программе, рост зародыша живого организма, пользование телефоном-автоматом являются примерами такой ситуации.
Однако случаи, когда управление u₀(t) без обратной связи, только по априорной информации, приводит к достижению цели, возможны лишь при том условии, что все будет происходить именно так, как предписывает заданная траектория.
^ EXTRACTION,
DETECTION
выявление

CLASSIFICATION
классификация

VARIABLE
переменная

ORIGIN
происхождение

CONTROL
управление

Разделение рассматриваемого множества объектов на классы является первым, простейшим актом моделирования этого множества. Как и всякая модель, классификация, отражая объективные различия, в то же время носит целевой характер и является относительной, условной. Поэтому возможны разнообразные классификации одного и того же множества. Это, конечно, относится и к множеству систем.

Чаще оказывается, что процессы на неуправляемых входах v₀(t) отличаются от ранее предполагаемых, либо существенным оказывается действие неучитываемых входов и система “сходит с нужной траектории”. Пусть имеется возможность наблюдать текущую траекторию y(t), находить разность y(t-) y₀(t) и определять дополнительное к программному управление, которое в ближайшем будущем возвратит выходы системы на нужную траекторию y₀(·). Такой способ управления называется регулированием, а соответствующие системы выделены во второй класс второго уровня классификации (рис. 4.5). Например, этому классу принадлежит управление, которое осуществляется операторами-станочниками, регулятором Уатта, автопилотом, судовым авторулевым, в рефлекторных реакциях животных и т.п.
Следующие способы управления и соответствующие им типы систем возникают в связи с необходимостью управления в условиях, когда либо невозможно задать опорную программную траекторию на весь период времени, либо уклонение от нее столь велико, что невозможно вернуться на нее (регулирование обычно осуществляется при “малых” в известном смысле уклонениях^* y(t-) y₀(t). Теперь нам необходимо спрогнозировать текущую траекторию y(t) на будущее и определить, пересечет ли она целевую область Y*. Управление состоит в подстройке параметров системы до тех пор, пока такое пересечение не будет обеспечено. Этому и соответствует третий класс систем. Примерами такого управления являются процессы адаптации живых организмов к изменяющимся условиям жизни, работа пилотов и шоферов, адаптивные и автоматизированные системы управления и т.п.