Основные типы локальных регуляторов

Множество локальных регуляторов можно упорядочить по различным признакам:

Во-первых, в зависимости от характера информации, используемой в регуляторе:

1.) С регулированием по разомкнутому циклу (по возмущениям).

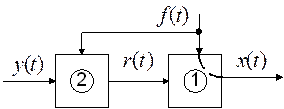
Проблема состояла в определении регулирующего воздействия.

Здесь регулятор настраивается в зависимости от основного возмущения .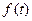

“+”: высокое быстродействие, так как регулятор настраивается сразу по возмущению, а не так, как в случае регулирования по замкнутому циклу.

“–”: трудность программирования регулятора на возможные возмущения, следовательно, невысокая точность.

2.) С регулированием по замкнутому циклу (по отклонениям).

“+”: в независимости от причин появления ошибки 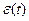, система работает по принципу её (ошибки) компенсации.

“–”: быстродействие ниже, чем в случае с регулированием по разомкнутому циклу.

3.) С регулированием по комбинированию.

Объединение случаев регулирования по разомкнутому циклу и по замкнутому циклу.

Во-вторых, в зависимости от уставки :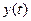

1.) Системы стабилизации .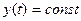

2.) Программные системы 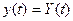, причём 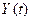— известно.

3.) Следящие системы 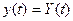, причём 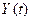— заранее неизвестная функция.

В-третьих, в зависимости от размерности n вектора состояния :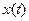

1.) Одномерные n = 1.

2.) Двумерные n = 2.

3.) Многомерные n = 3.

В-четвёртых, в зависимости от количества контуров в системе:

1.) Одноконтурные (используется только главная обратная связь, нет местных связей).

2.) Двухконтурные (используются одна главная и одна местная обратные связи).

3.) Многоконтурные (используются одна главная и много местных обратных связей).

В-пятых, в зависимости от установившегося значения ошибки:

1.) Статические .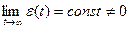

2.) Астатические .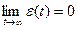

Систему называют астатической по управляющему (или возмущающему) воздействию, если при подаче на вход постоянного управляющего (или возмущающего) воздействия ошибка в установившемся состоянии не зависит от величины этого воздействия и равна нулю.

Сравнить рисунки 24 и 26 методических указаний.

В-шестых, в зависимости от характеров сигналов, циркулирующих в системе:

1.) Непрерывные.

2.) Импульсные.

3.) Релейные.

4.) Релейно-импульсные (кодово-импульсные).

5.) На переменном токе (с гармонической модуляцией).

1.) В непрерывных системах сигналы могут быть описаны непрерывными во времени функциями.