Сила, действующая на тело в потоке воздуха
Обращаясь к рассмотрению сил, действующих на паруса, мы будем отвлекаться от других сил, которые действуют на корпус и подводные плавники. Будем рассматривать парус как неподвижное тело, помещённое в набегающий поток воздуха, независимо от того, чем образован этот поток, ветром или собственным движением судна. Поток воздуха характеризуется скоростью V, которая может меняться от точки к точке при обтекании тела. Как материальная среда, воздух наделён определённой плотностью ρ, которая характеризует массу единицы объёма воздуха (1,25 кг на кубометр). Каждая частица движущегося воздуха обладает кинетической энергией, плотность которой* зависит от скорости воздуха в данной точке и равна
q = ½ ρ V2.
Кинетическая энергия является мерой давления*, которое оказывает поток на поставленную попрёк него преграду. Сила, действующая на парус, образуется за счёт того, что он, притормаживая воздушный поток, отбирает от него часть этой энергии.
Явления, происходящие при обтекании тел водой, ничем существенным не отличаются от явлений обтекания воздухом. Различие состоит лишь в величине плотности ρ, которая у воды в 800 раз выше чем у воздуха., а также в несколько большей вязкости воды. Поэтому при чтении данного раздела следует иметь в виду, что все рассуждения справедливы не только для паруса, но и для частей корпуса, обтекаемых водой, (с поправкой на увеличение сил в 800 раз). Этим обстоятельством мы воспользуемся в дальнейшем, когда при рассмотрении гидродинамики судна будем считать, что общие законы обтекания нам известны из теории паруса.
Рассмотрим сначала, какие силы действуют на тонкую плоскую пластину в потоке воздуха.
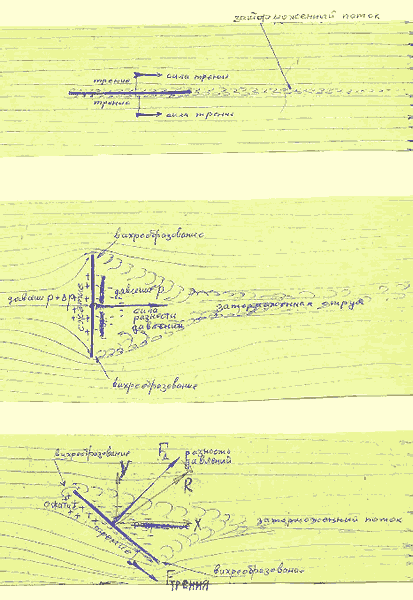
Рис. 3.2.
Пластина, поставленная вдоль воздушного потока (рис. 3.2), показывает возникновение силы сопротивления даже при минимальном поперечном сечении тела. Слой воздуха, прилегающий к пластине, затормаживается из-за трения о неподвижную поверхность тем сильнее, чем больше площадь пластины S. Кинетическая энергия заторможенной струи переходит в тепловую энергию трения, а инерция струи передаётся парусу и тянет его в направлении потока с силой
F = C q S = C ½ ρ V2 S
В этой формуле С – так называемый коэффициент аэродинамической силы, который указывает, какая доля энергии потока преобразуется в энергию паруса. Этот коэффициент зависит от формы паруса и других условий обтекания, являясь исчерпывающей характеристикой его полезной работы. Можно сказать, что вся теория паруса сводится к изучению влияния различных факторов на величину С.
Если пластину поставить поперек потока (рис. 3.2 б), то на нее будут воздействовать два механизма, приводящие к возникновению аэродинамической силы. Во-первых, перед пластиной воздушный поток затормаживается из-за того, что пластина препятствует движению потока. В результате энергия движения потока переходит в энергию статического давления, которая приводит к возникновению разности давления Δр по сторонам пластины.
Второй механизм образования силы лобового сопротивления может быть истолкован как потеря кинетической энергии воздушного потока при перетекании его через края пластины. Здесь происходит интенсивное взаимодействие воздуха с препятствием, вихреобразование и торможение.
При косом расположении пластины (рис. 3.2 в), на ней образуется как сила трения Fтр, действующая вдоль поверхности пластины, так и сила разности давлений FN,действующая перпендикулярно пластине (подъёмная сила). Поскольку сила трения много меньше силы разности давления, суммарная сила R также направлена почти перпендикулярно поверхности пластины. Важно то, что сила имеет две составляющие не только X – силу лобового сопротивления, но также Y – так называемую подъемную силу, направленную поперек воздушного потока. Эту силу можно также объяснить как реактивную силу воздушной струи, отклоненной поперек своего первоначального движения. За счет существования этой поперечной силы и возможно использование паруса для движения не только по ветру, но даже и против ветра.
Однако плоская пластина является мало эффективным парусом и развивающаяся на ней подъемная сила сравнительно невелика. Больший эффект получается при использовании плавно изогнутых профилей. Рассмотрим обтекание несимметричного профиля воздушным потоком в канале (трубе) на рис. 3.3.
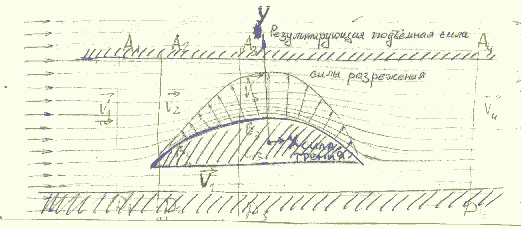
Рис. 3.3.
Скорость потока в сечениях канала А1Д1 и А4Д4 (до вставленного в канал тела и после него) равны друг другу V1 = V4, (если пренебречь незначительными завихрениями). Но в сечении А3Д3 ширина канала значительно уменьшена. Следовательно для того, чтобы через него проходил тот же поток, необходимо чтобы скорость в равной степени возросла: V3 > V1.. При этом с плоской стороны профиля остается скорость, равная V1, так как поток, входящий в эту часть канала с начальной скоростью V1 в сечении С2Д2, где влияние вставленного тела еще не ощущается, должен сохранить эту скорость и на всем протяжении этой части канала из-за однородности сечения.
Таким образом мы видим, что с выпуклой стороны тела скорость обтекающего потока оказывается больше, чем со стороны плоской поверхности. Это значит, что плотность кинетической энергии потока с выпуклой стороны увеличивается. Согласно закону сохранения энергии это увеличение может происходить только за счёт какой-либо другой энергии. В данном случае в потоке нет другого источника, кроме энергии барометрического давления, которая и переходит в энергию движения потока на выпуклой стороне. Следовательно в том месте профиля, где возрастает кинетическая энергия и скорость потока, там уменьшается барометрическое давление. Оно становится тем меньше, чем больше ускоряется обтекающий поток. Другими словами на выпуклой поверхности возникает разрежение, которое «засасывает в себя» обтекаемый воздухом профиль. Силы этого «засасывания» показаны графически на рисунке. Они действуют перпендикулярно поверхности тела, их сумма Y направлена поперёк набегающему потоку и представляет собой чистую «подъёмную» силу. Эти силы, возникающие в результате несимметричного обтекания, значительно превосходят силы, обусловленные трением. Если учесть на рис. 3.3 также и силу трения Х, то она даст незначительную горизонтальную составляющую по сравнению с подъёмной силой Y.
Обтекание несимметричного профиля для удобства рассуждений было рассмотрено в случае, когда он помещён в достаточно узкий канал, но очевидно, что в свободном пространстве характер обтекания существенно не изменится. Поэтому останутся справедливыми и сделанные выводы.
3.1.2. Подъёмная сила и лобовое сопротивление паруса
Простейшей моделью работы паруса является обтекание плоской пластины, изображённое на рис. 3.2. Однако в результате действия разности давлений по сторонам материала паруса он теряет плоскую форму и образует в сечении плавно изогнутый профиль. Это изменение формы натянутой парусины является полезным эффектом, так как в результате плавного обтекания воздухом образуется меньше завихрений чем на плоской пластине, и подъёмная сила на парусе возрастает за счёт падения давления при обтекании воздухом выпуклой поверхности, как то объяснено в предыдущем параграфе. Чем меньше при этом образуется вихрей, тем на большей части паруса происходит плавное обтекание подветренной выпуклой стороны, и тем бóльшая образуется разность давлений, приводящая к бóльшей подъёмной силе. Что касается силы лобового сопротивления, то она от выдувания плоской поверхности практически не зависит.
Распределение сил трения, давления и разряжения по поверхности реального паруса показано на рис. 3.4.
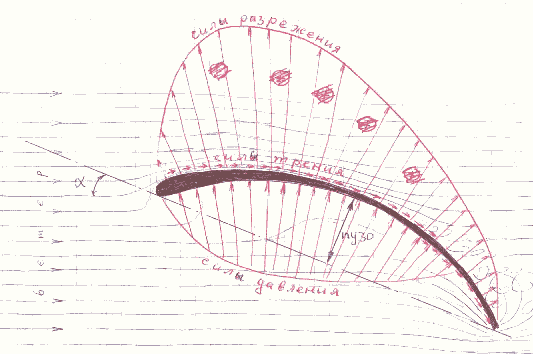
Рис. 3.4.
Суммарная результирующая аэродинамическая сила на парусе правильной формы имеет бóльшую величину и направлена более перпендикулярно к ветровому потоку, чем аэродинамическая сила на плоской пластине. Отклонение поверхности паруса от плоскости под ветер называется пузом паруса и является одной из важнейших характеристик конструкции паруса, которая влияет на его качество и способность обеспечить надлежащую тягу в нужном направлении.
Главным же образом величина и направление аэродинамических сил на парусе зависит от его положения относительно потока воздуха, которое характеризуется углом атаки α (см. рис. 3.5).
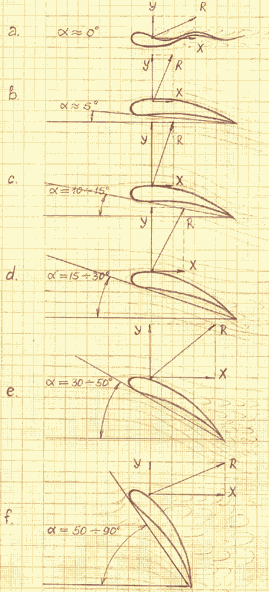
Рис. 3.5.
Даже при очень малых углах атаки, и при α =0˚, на профиле, имеющем аэродинамическое пузо, как мы видели на рис. 3.3, развивается определённая подъёмная сила, которая тем больше, чем больше величина пуза. Но реальные мягкие паруса на углах атаки около 0˚ не сохраняют аэродинамической формы, а начинают заполаскивать, что приводит к почти полной потере подъёмной силы при сохранении и даже увеличении силы лобового сопротивления (рис. 3.5 а). При увеличении угла атаки до 10˚ - 15˚ подъёмная сила резко увеличивается, в то время как лобовое сопротивление остаётся практически на исходном уровне. В диапазоне углов атаки 20˚ - 30˚ подъёмная сила перестаёт расти, но начинает сильно расти лобовое сопротивление, и результирующая суммарная сила увеличивается. Для некоторых типов парусов суммарная сила принимает наибольшее значение при углах атаки 30˚ - 50˚, но направлена она уже в большей степени не поперёк, а вдоль потока воздуха при снижении подъёмной силы. И наконец, при 50˚ - 90˚ подъёмная сила постепенно исчезает, а лобовое сопротивление слабо возрастает, достигая максимума. Однако общая сила при этом имеет тенденцию к снижению из-за исчезновения подъёмной силы.
Изображать зависимость от угла атаки сил, действующих на парус, удобно на специальном графике, называемом полярой (рис. 3.6).
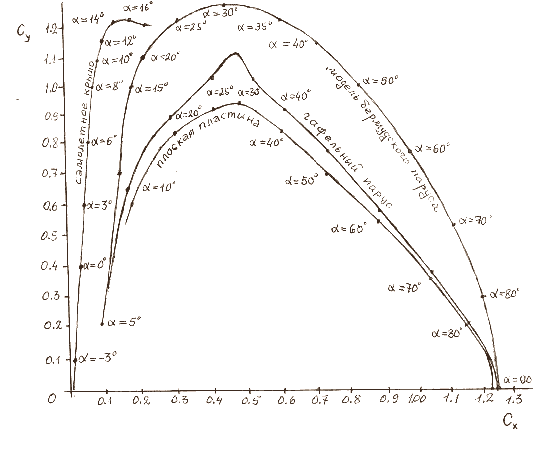
Рис. 3.6.
На нём каждая точка кривой имеет горизонтальную координату, равную лобовому сопротивлению Х, вертикальную координату, равную подъёмной силе Y, а значение угла атаки нанесено на самой кривой. Для сравнения эффективности парусов различного размера на поляре показывают не абсолютные значения сил (в килограммах), а величины, отнесённые к площади паруса. В качестве таких величин приняты коэффициенты аэродинамических сил, показывающие, какая доля энергии потока, падающего на единицу поверхности паруса, преобразуется в ту или иную составляющую суммарной силы. Различают: коэффициент результирующей силы СR, коэффициент подъёмной силы СY и коэффициент лобового сопротивления СХ. Вспоминая, что плотность кинетической энергии потока равна ½ ρ
V2 , где ρ – плотность воздуха, V – скорость потока, мы можем написать выражения для расчёта абсолютных значений аэродинамических сил:
тяга R = СR ½ ρ V2 S
лобовое сопротивление Х = СХ ½ ρ V2 S
подъемная сила Y = СY ½ ρ V2 S
На рис. 3.6 показаны примеры поляр для различных парусов и самолётного крыла. Из сравнения графиков мы можем сделать следующие выводы:
а) Жёсткое самолётное крыло сохраняет подъёмную силу при малых (меньше 5˚) и даже небольших отрицательных углах атаки, там где мягкий парус работать не может. При этом лобовое сопротивление крыла существенно меньше, чем достижимо для паруса. Следовательно, если бы судно было оборудовано жёстким крылом, то при слишком сильном ветре, когда уже необходимо убирать паруса, жёсткое крыло могло бы быть поставлено в такое положение, что ветер на него не оказывал бы чрезмерного воздействия.
б) При углах атаки вплоть до 20˚ крыло имеет бóльшую подъёмную силу чем парус.
в) Правильно сконструированный парус может обеспечить бóльшую величину аэродинамических сил, чем типичное самолётное крыло равной площади.
г) Наибольшие значения аэродинамических сил паруса достигаются при бóльших значениях угла атаки чем у самолётного крыла.
д) Паруса современных яхт (бермудские) эффективнее, чем классические типы парусов времён парусного флота (плоский гафельный парус).
е) Плоская пластина является наихудшим типом паруса.
Объяснение этих выводов, а также факторы, влияющие на эффективность паруса, рассматриваются в следующем разделе.
Дата добавления: 2014-12-29; просмотров: 3970;
