Понятие о векторе. Правило сложения векторов.

Векторные величины в отличие от скалярных характеризуются, помимо абсолютной величины, также и направлением. Примером могут служить скорость, ускорение, электрический ток и т. д. Выб­рав определенный масштаб, векторные величины можно изобра­жать отрезками прямых со стрелкой, указывающей направление векторной величины. Длина отрезка прямой в определенном масштабе указывает на абсолютную величину данной векторной величины.

ЭДС является векторной величиной, т. е. характеризуется вели­чиной и направлением. Она может быть изображена в виде отрез­ка прямой со стрелкой, или вектора. Длина вектора в определенном масштабе отражает размеры ЭДС, например 3 мВ. Стрелка вектора говорит о направлении ЭДС. При обозначении ЭДС начало вектора соответствует минусу, конец — плюсу. Век­торные величины могут быть направлены в одну или в разные стороны. Правила сложения векторов дают возможность определить сум­марный, или результирующий, вектор. Векторы складываются, как алгебраические величины. Например, два вектора (а и б) распо­ложены параллельно и направлены в одну сторону. Суммарный вектор будет представлять собой сумму этих двух векторов и направлен в ту же сторону. Если два вектора (а и б) расположены параллельно и направлены в противоположные сто­роны, суммарный вектор будет направлен в сторону большего вектора и представлять собой разность между двумя век­торами: из большего вектора (а) вычитается меньший вектор.

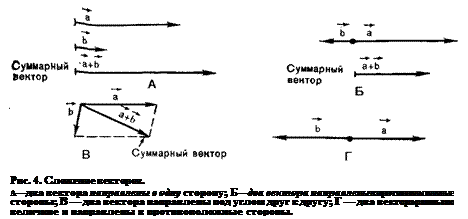
Если два вектора (а и б) направлены под углом друг к другу, их располагают так, чтобы они исходили из одной точки. Затем, считая, что такие векторы образуют две стороны параллелограмма, достраивают параллелограмм и проводят диа­гональ из точки, где совмещены начала обоих векторов. Диагональ параллелограмма и будет представлять собой сумму двух векто­ров, или суммарный вектор. Если два вектора равны по величине и направлены в противоположные стороны суммарный вектор будет равен нулю.