Координаты, определяющие положение ракеты в пространстве

При решении различных задач, связанных с расчетом траек­тории ракеты, с устойчивостью движения, с тепловыми и проч­ностными расчетами, возникает необходимость вводить системы отсчета времени и положения ракеты в пространстве.

Отсчет времени, принятый в ракетной технике, является единым и независимо от рассматриваемых задач ведется от момента старта ракеты. Поэтому, если в описании каких-то операций, производимых в связи с подготовкой к старту, или же при указании определенного события мы встречаем выражения типа: «Зажигание производится в момент Т — — 00 : 00 : 06,4 сек» или «Команда на повторный запуск прошла в Т + 02 : 44 : 18,0 сек», то это означает, что первая операция производится за 6,4 сек до, а вторая — через 2 часа

44 мин 18 сек после старта. Под Т понимается обычно астрономическое время. Момент отрыва ракеты фиксируется срабатыванием контакта подъема, в результате чего поступает сигнал для службы единого времени всех наземных средств и бортовых систем.

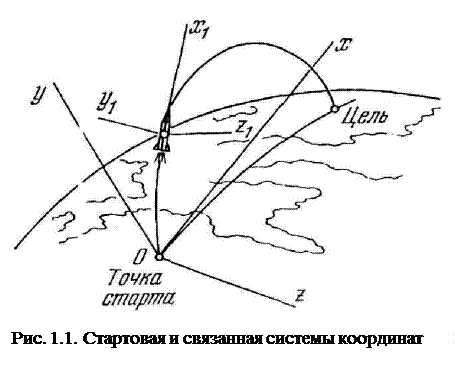
Положение ракеты как материальной точки в пространстве определяется прежде всего тремя координатами х, у, z в так называемой баллистической (стартовой) системе координат, связанной с Землей. За начало этой системы берут точку старта ракеты. Для баллистических ракет за ось х принимают пря­мую, перпендикулярную к ра­диусу вектору из центра Зем­ли и направленную по линии прицеливания в сторону цели (рис. 1.1). Ось у направляют по радиусу вектору вверх, а z — перпендикулярно двум пер­вым осям так, чтобы система координат была правой.

Система х, у, z не является инерциальной, поскольку связана с Землей, совершающей суточное вращение. Это означает, что при определении траектории в этой системе необходимо в общем случае учитывать кориолисово и переносное ускорения. Впрочем, для удобств оценки влияния вращения Земли можно ввести и другую систему х₀, у₀, z₀, полностью совпадающую с системой х, у, z, но остающуюся неподвижной с момента стар­та ракеты. Этой системой мы воспользуем­ся позже, а пока вращение Земли учиты­вать не будем.

Введем еще так называемую связанную или подвижную систему осей. Начало ее поместим в центре масс ракеты, а оси x₁, y₁, z₁свяжем с характерными геометриче­скими элементами ракеты. Ось x₁направлена по продольной оси ракеты. Оси y_1, z₁расположим в плоскости, перпендикулярной оси ракеты, так, чтобы на старте плоскость x₁y₁совпадала с плоскостью ху земной системы координат, а ось z₁ имела то же направление, что и ось z. Ось y₁ называют поперечной, a z₁ - боковой осью (рис. 1.1 и 1.2).

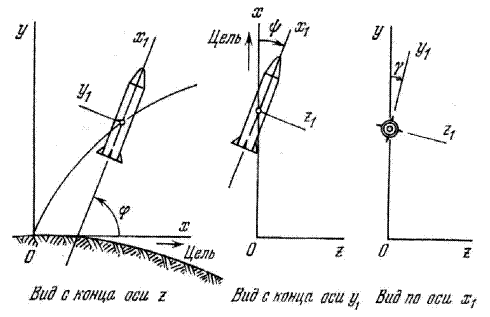
Для полного определения положения ракеты в пространстве как жесткого тела в дополнение к координатам х, у, z вводят еще три угла, определяющие взаимную ориентацию осей связан­ной и стартовой систем координат. Угол между осью ракеты х₁и плоскостью xz, т. е. угол наклона оси ракеты по отношению к стартовому горизонту, обо­значим через φ. Этот угол называют углом тангажа (рис.1.3)

.

Угол, который составляет ось ракеты х₁ с плоскостью ху, обо­значим через ψ. Его называют углом рыскания. Он характери­зует отклонение оси ракеты от плоскости х,у.

Введем, наконец, еще один угол, определяющий поворот корпуса ракеты относительно ее продольной оси – угол крена γ между осью y₁и пло­скостью ху.

Таким образом, три координаты xyz и три угла φ, ψ и γ (см. рис. 1.3) полностью определяют поло­жение ракеты в пространстве.

Наряду с рассмотренными систе­мами координат для удобства веде­ния аэродинамических расчетов на атмосферных участках полета вво­дится еще так называемая поточ­ная (скоростная) система x₂, y₂, z₂. Ось x₂ направлена по вектору ско­рости полета v, т. е. по касатель­ной к траектории; ось y₂ — по главной нормали к траектории, а ось z₂ — перпендикулярно двум первым (рис. 1.4).

Связанная и поточная системы осей, вообще говоря, не со­впадают. В вертикальной плоскости ось ракеты x₁ образует с проекцией вектора скорости угол α, который, как мы уже знаем, назы­вается углом атаки, а с плоскостью x₂y₂— угол β, который называется углом скольжения (рис. 1.4). На атмосферном участ­ке полета баллистических ракет эти углы весьма малы. Мы уже говорили, что угол атаки на атмосферном участке не превышает 1—2°. Что же касается угла скольжения, то его номинальное значение и вовсе считается равным нулю. Важен не сам угол, а его отклонения от номинала ±Δβ, учитывать которые необхо­димо при анализе устойчивости движения.

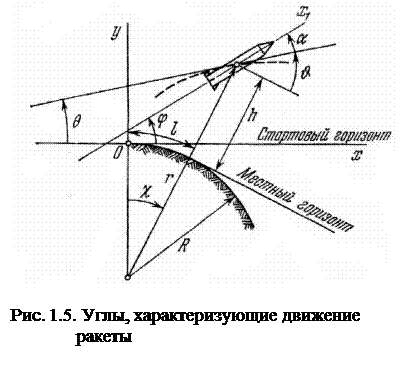И, наконец, для последующего, более экономного вывода уравнений движения введем еще полярную систему координат r, х (рис. 1.5) с полюсом в центре Земли, форму которой прини­маем сферической. Кроме полярного угла χ и радиуса r, здесь через θ обозначен угол между касательной к траектории и стар­товой осью х, а через υ - угол между той же касательной и линией местного горизонта; r — R = h — вы­сота полета, R — радиус Земли. Величина l = R_χ называется ортодромной (Ортодрома — линия дуги большого круга на поверхности сферы) дальностью.