Силы, действующие на ракету

Рассмотрим систему ос­новных сил, действующих на ракету в полете.

Основными силами, оп­ределяющими движение центра масс ракеты, являются: сила тяги, собственный вес ра­кеты, аэродинамические силы и силы на управляющих органах. Как и всякое тело, движущееся в воздухе, газе или жидко­сти, ракета испытывает со стороны среды действие сил трения и давления на поверхности. Значения этих сил и законы их распределения зависят от многих факторов и в первую очередь от скорости полета. Статическая составляющая сил атмосфер­ного давления уже была нами учтена при выводе выраже­ния тяги (1.5). Поэтому при определении аэродинамических сил необходимо рассматривать лишь увеличение давления по срав­нению со статическим у головной части и его понижение у донного среза. Это избыточное (положительное или отрицательное) давление вместе с силами аэродинамического трения дает рав­нодействующую, которая называется полной аэродинамической силой.

При анализе законов движения ракеты и вообще летатель­ного аппарата полную аэродинамическую силу раскладывают обычно по скоростным осям x₂, у₂ и z₂ на составляющие X, Y, Z.

Составляющая X полной аэродинамической силы по каса­тельной к траектории (или ее проекция на направление вектора скорости) называется лобовым сопротивлением. Эта сила все­гда направлена в сторону, противоположную вектору скорости полета.

Составляющая Y полной аэродинамической силы по поточ­ной оси у₂называется подъемной силой, а составляющая Z — боковой силой.

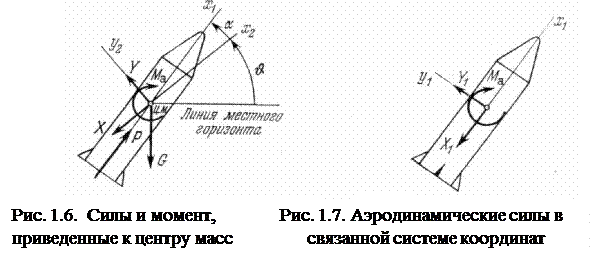На рис. 1.6 показаны сила тяги Р, направленная по оси ра­кеты, сила веса G — Mg по местной вертикали, а также состав­ляющие аэродинамической силы X и Y.

Прежде чем замкнуть полученную систему сил усилиями от управляющих органов, заметим, что полная аэродинамическая сила может быть разложена также не по поточным, а по свя­занным осям x₁, y₁, z₁. Такое разложение представляет опреде­ленные удобства не только при баллистических расчетах, но и при определении нагрузок, действующих на элементы конструк­ции.

Составляющие полной аэродинамической силы соответствен­но осям x₁, y₁, z₁ обозначаются X₁, Y₁, Z₁и называются осевой или продольной, нормальной и поперечной аэродинамическими силами. На рис. 1.7 показаны осевая X₁ и нормальная Y₁ силы. Из сопоставления сил и углов (рис. 1.6 и 1.7) легко установить, что при отсутствии скольжения (при β = 0)

X₁ = X cos α – Y sin α, Y₁ = Y cos α + X sin α,

или в обратной форме

X = X₁ cos α + Y₁ sin α, Y = Y₁ cos α – X₁ sin α (1.1)

Система распределенных по поверхности ракеты аэродина­мических сил согласно законам механики приводится не только к полной аэродинамической силе, но и к моменту, величина которого зависит от точки приведения сил. Приводя силы к центру масс, мы, кроме упомянутых составляющих X, Y, Z, по­лучаем аэродинамический результирующий момент, который аналогично вектору полной аэродинамической силы может быть разложен по осям x₁, y₁, z₁или x₂, y₂, z₂.На рис. 1.6 и 1.7 пока­зана составляющая этого момента в плоскости x₁y₁ связанной системы координат. Более подробно об этих моментах мы пого­ворим позже. Итак, нам осталось к силам, показанным на 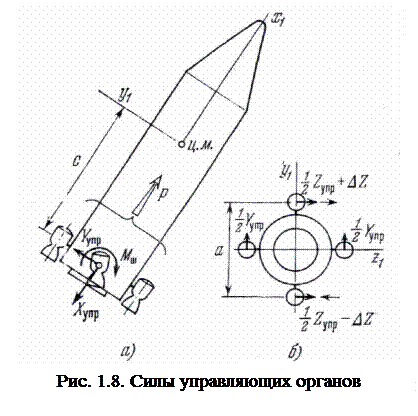рис. 1.6, добавить систему сил от органов управления. Эти силы удобно приводить к осям, относительно кото­рых осуществляется поворот управляющего органа.

В результате в связанной системе координат получаем суммарные составляющие Х_упр и Y_упр (рис. 1.8, а). Первая из этих сил Х_упрне является управляющей и на­зывается потерей тяги на органах управления. Вторая сила Y_упр представляет со­бой управляющую силу; она создает момент относитель­но центральной поперечной оси z₁. Плечо этого момента равно расстоянию с (рис. 1.8, а) от шарнира до центра масс ракеты.

В том случае, когда ракета управляется газоструйными ру­лями, силу Х_упр по аналогии с аэродинамическими силами называют сопротивлением рулей, а силу Y_упр — подъемной силой рулей. Если же управляющими органами являются поворотные камеры, то их суммарная тяга включается в общую тягу двига­тельной установки, а под Х_упр опять же понимается потеря, свя­занная с тем, что при повороте камеры ее тяга направлена не по оси ракеты.

Приводя силы к оси поворота управляющего органа, мы получаем, естественно, и момент, который воспринимается руле­вой машиной и называется шарнирным моментом М_ш (рис. 1.8, а).

Совершенно очевидно, что аналогичное управляющее усилие Z_упр создается и в плоскости x₁z₁, Эта сила Z_ynp дает момент относительно оси y₁(рис. 1.8,б).

Наконец, для того чтобы создать управляющий момент относительно продольной оси x₁, необходимо для одной пары рулей или управляющих камер предусмотреть поворот в противофазе. В результате возникает необходимый управляющий момент ΔZa (рис. 1.8,б).

Расположение осей поворота рулей или камер, показанных на рис. 6.8,б , не является обязательным. Возможны и другие схемы поворота камер. Важно лишь, чтобы органы управления обеспечивали создание моментов относительно всех трех осей x₁, y₁, z_1.

Теперь мы имеем систему основных сил и можем обра­титься к составлению уравнений движения ракеты.