Статический и демпфирующий моменты
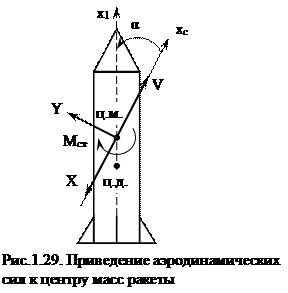
Известно, что система распределённых по поверхности аэродинамических сил по правилам механики может быть приведена к любой точке ракеты в виде главного вектора с составляющими Х и Y и момента Ма , величина которого зависит т точки приведения. В центре давления величина момента Ма равна нулю, так как это точка приложения главного вектора аэродинамических сил (рис. 1.29 и рис. 1.30).
Момент аэродинамический разбивается на два слагаемых:
первое - статический или позиционный момент Мст ;
второе – демпфирующий момент МД .
Статический момент определяется как функция угла атаки при нулевой скорости вращения и зависит от ориентации ракеты по отношению к потоку, т.е. от позиции, которую она занимает в потоке. Если Мст направлен в сторону уменьшения угла атаки, то он называется восстанавливающим или стабилизирующим моментом. При обратном направлении его называют опрокидывающим или дестабилизирующим (рис. 1.29).

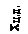
Выражение для момента Мст строится по тому же принципу, что и для лобового сопротивления и подъёмной силы:
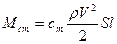 ,
,
где сm – безразмерный коэффициент статического момента;
S – площадь миделя;
l – характерная длина (для ракеты принимается её длина).
Безразмерный коэффициент статического момента в первом приближении представляет собой производную от коэффициента сm по α и является функцией только числа Маха.
Значение демпфирующих моментов МД зависит от угловой скорости вращения ракеты относительно любой оси. Демпфирующие моменты всегда направлены в сторону, противоположную вращению, и в первом приближении пропорциональны угловой скорости.
 |
Возникновение демпфируюших моментов и их величина зависит от условий обтекания и от течения масс жидкости и газа во внутренних полостях ракеты. В соответствии с этим различают внешние и внутренние демпфирующие моменты (рис. 1.31 и 1.32).
Выражение для демпфирующего внешнего (аэродинамического) момента имеет вид
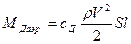 .
.
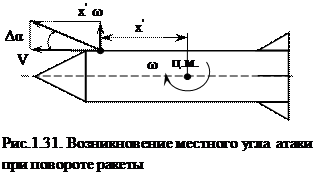
В каждой точке поверхности при повороте ракеты с угловой скоростью ω возникает местный угол атаки Δαм (рис.1.31), приводящий к аэродинамической силе и моменту относительно центра масс. Момент направлен против вращения.
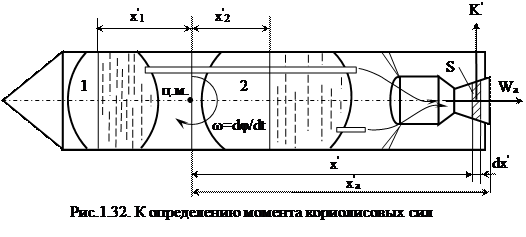
Демпфирующий внутренний момент возникает от действия кориолисовых сил (рис.1.32). Внутри ракеты перемещаются массы жидкости и газа. Элементарный момент кориолисовых сил для массы газа ρSdx', движущейся по соплу, выражением 2W(dφ/dt)ρS(dx')x', где ρWS – постоянный для всех сечений секундный расход массы.
Выражение для демпфирующего внутреннего момента (от действия Кориолисовых сил) строится с точностью до безразмерного множителя, называемого в данном случае коэффициентом демпфирующего момента:
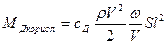 .
.
 |
Скорость V введена в числитель и знаменатель для того, чтобы в выражении момента в явном виде вошел скоростной напор. Под величиной ω понимается, в частности, скорость изменения угла тангажа φ.
Демпфирующий внутренний момент от действия кориолисовых сил в уравнениях движения ракеты обычно не учитывается; его влияние на законы движения ничтожно мало, но он рассматривается как самостоятельное слагаемое в оценке тех моментов, преодоление которых возлагается на рулевые органы.
Аэродинамические моменты – статический и демпфирующий – казалось бы малы, но от них зависит то, какими быть органам управления, какую тягу должны давать рулевые камеры, на какой угол им поворачиваться и какими параметрами должны обладать рулевые органы.
Дата добавления: 2014-12-26; просмотров: 5684;
