Порядок расчета нетто-ставки

Если условия страхования имущества содержат несколько видов страховой ответственности (например, от пожара, хищения, поломки и т.н.), то совокупная нетто-ставка может отражать каждый вид страховой ответственности, которую взял на себя страховщик, в виде нескольких нетто-ставок. Целый ряд рисков имеет различное происхождение. Например, риск «пожар» может произойти от удара молнии, замыкания электросети, поджога и взрыва. В этом случае нетто-ставка рассчитывается по каждой из причин пожара и суммируется в единую нетто-ставку по риску «пожар».

Кроме того, на размер нетто-ставок влияют и другие факторы имущественного страхования. Например, уникальность имущества (японские кинокамеры, египетские вазы, предметы антиквариата, картины и другие объекты, требующие особого подхода к их оценке), финансовое состояние заемщика кредита или предпринимателя, страхующегося от потери прибыли, вероятность и тяжесть ущерба (страхование банкиров, предпринимателей от несчастного случая на крупные страховые суммы).

Методика расчета нетто-ставки как составляющей части тарифа по каждому виду или однородным объектам страхования сводится к определению среднего показателя убыточности страховой суммы за тарифный период с поправкой на величину рисковой надбавки.

Нетто-ставка равна: убыточность страховой суммы плюс рисковая надбавка.

Убыточность определяется как соотношение суммы всех выплат по заключенным договорам страхованияк общей страховой сумме. Этот показатель носит интегральный характер и позволяет учитывать все многообразие факторов, которые влияют на наступление страховых событий и страховые выплаты:

g = W / S, (1)

где g – убыточность страховой суммы;
S – страховая сумма;
W – сумма выплат.

Убыточность можно также представить как произведение вероятности наступления страхового случая на отношение средней страховой выплаты к средней страховой сумме по договорам страхования. При этом вероятность наступления страхового случая определяется на основе статистических данных и характеризует закономерности конкретного вида страхования.

Убыточность страховой суммы — это отношение совокупной суммы страховых выплат к совокупной страховой сумме:

g = W_св / S_сс, (2)

где g – убыточность страховой суммы;
W_св – совокупная сумма страховых выплат;
S_сс – совокупная страховая сумма.

Убыточность страховой суммы как соотношение денежных показателей является величиной синтетической, зависит от действия различных факторов, влияющих на убыточность страховой суммы, называемых элементами убыточности.

Частоту страховых событий (вероятность наступления страхового случая иногда называют коэффициентом горимости) определяют путем отношения числа страховых случаев к числу объектов страхования:

f_c/c = M / N, (3)

где f_c/c – частота страховых событий;
M – число страховых случаев;
N – число объектов страхования.

Вероятность страхового случая – количественная оценка возможности наступления и периодичности страховых случаев для отдельных объектов страхования, по которым выплачивается страховое возмещение. Служит основой для установления страховых тарифов, вычисляется с применением теории вероятности и закона больших чисел.

Опустошительность одного страхового случая есть отношение числа пострадавших объектов к числу произошедших страховых случаев:

О_опуст = N_п / M, (4)

где О_опуст – опустошительность одного страхового случая;
N_п – число пострадавших объектов;
M – число произошедших страховых случаев.

Тяжесть ущерба есть отношение выплачиваемого ущерба к числу страховых случаев:

Т_у = SC_в / M, (5)

где Т_у – тяжесть ущерба;
SC_в – выплачиваемый ущерб;
M – число страховых случаев.

Нетто-ставки в имущественном и личном страховании имеют следующие особенности: нетто-ставка имущественного страхования состоит из рисковой части и стабилизационной надбавки (Δ-надбавки). При личном страховании нетто-ставка включает рисковую часть для рисковых видов личного страхования, например несчастный случай, смерть и смерть от несчастного случая, страхование на случай смерти, и накопительную часть по риску накопительным и смешанным видам личного страхования.

Величина частных нетто-ставок исчисляется в прямой зависимости от вероятности риска. Однако поскольку страховой взнос есть усредненный размер данных страховых платежей, возможны существенные отклонения от средних значений.

Убыточность страховой суммы не может быть одинакова на протяжении ряда лет. Поэтому для правильного определения нетто-ставки необходимо определить меру устойчивости данного показателя путем использования среднеквадратичного отклонения за ряд лет.

Полученное отклонение называют рисковой надбавкой. Ее цель — создать устойчивость ежегодных результатов в рамках страхования каждого вида имущества. Рисковая надбавка повышает устойчивость результатов страхования путем увеличения размера страховых тарифов:

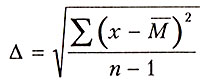(6)

где Δ – среднеквадратическое отклонение (рисковая надбавка);
x – убыточность страховой суммы какого-либо года;
М – средняя арифметическая величина убыточности страховой суммы за ряд лет;
n – число лет наблюдения.

Нетто-ставка рассчитывается по формуле (7):

Нетто-ставка = М + Δ, (7)

где Δ – среднеквадратическое отклонение (рисковая надбавка);
М – средняя арифметическая величина убыточности страховой суммы за ряд лет.

Использование для рисковой надбавки величины среднеквадратического отклонения связано с установленной теорией статистики закономерности, согласно которой при М + Δ вероятность того, что в будущем фактические показатели убыточности окажутся меньше размера нетто-ставки, составляет 68%. При М + 2 Δ та же величина равна 95%.

Для получения лицензии на возможность осуществления нового вида страхования страховая компания среди прочих документов должна предоставить экономическое обоснование размера тарифных ставок.

Страховая компания при подготовке нового вида страхования не имеет своих данных относительно вероятности и ожидаемой величины ущерба. Это заставляет страховщиков использовать внешние источники информации. Например, при подготовке страхования автомобилей необходимые сведения о частоте дорожных происшествий можно получить в управлении Государственной инспекции безопасности дорожного движения; для огневого страхования требуемые показатели могут быть рассчитаны на основе информации управлений государственной пожарной службы и т.д. Однако, как правило, полученных из таких источников данных недостаточно для оценки параметров величины выплат и страховых сумм. В методике расчета тарифных ставок по рисковым видам страхования (распоряжение Росстрахнадзора № 02-03-36 от 8 июля 1993 г.) приводятся рекомендации относительно выбора величины соотношений средней выплаты к средней страховой сумме:

· 0,3 — при страховании от несчастных случаев и болезней в медицинском страховании;

· 0,4 — при страховании средств наземного транспорта;

· 0,5 — при страховании грузов и имущества, кроме средств транспорта;

· 0,6 — при страховании средств воздушного транспорта;

· 0,7 — при страховании ответственности владельцев автотранспортных средств и других видов ответственности и страховании финансовых рисков.

Пользуясь предложенными рекомендациями по выбору соотношений, страховщик, рассчитывая тариф по конкретному виду страхования, подбирает величину средней страховой суммы S по рассматриваемому объекту и соответственно среднюю величину выплат S_в.

Основная часть нетто-ставки Т_о соответствует средним выплатам страховщика, зависящим от вероятности наступления страхового случая g, и рассчитывается по формуле 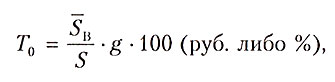(8):

, (8)

где Т_о – основная часть нетто-ставки;
S_в – средняя величина выплат;
S – страховая сумма;
g – вероятность наступления страхового случая.

Расчет рисковой надбавки ведется по формуле (9):

, (9)

где у – вероятность непревышения возможных выплат над собранными взносами;
а(у) – коэффициент, зависящий от гарантии безопасности;
а – показатель, который с вероятностью у гарантирует превышение собранных премий над выплатами;
n – квантиль нормального распределения.

Значение а зависит от вероятности у: чем выше требуемая гарантия безопасности, тем больше будет a. Ниже приведена таблица значений а для часто используемых значений гарантии безопасности.

Значения а для часто используемых значений гарантии безопасности:

Например, если величину гарантии безопасности у принять 98%, то для определенной величины страхового фонда к ожидаемой величине убытков необходимо прибавить двойное среднеквадратическое отклонение суммы выплат a.

Так как страховщик не заключил ни одного договора страхования, в этой формуле в качестве n будет присутствовать прогнозируемое число договоров данного типа. При увеличении n значение a зависит от вероятности у: чем выше требуемая гарантия безопасности, тем больше будет а, рисковая надбавка уменьшается, что ведет к снижению тарифов. Поэтому не следует завышать планируемое число договоров, поскольку это может привести к занижению тарифных ставок и, как следствие, к нехватке средств страхового фонда и возможному банкротству по данному виду страхования.